import sklearn.datasets as sk_data
X, y, gt_centers = sk_data.make_blobs(n_samples=100, centers=3, n_features=30,
center_box=(-10.0, 10.0), random_state=0, return_centers=True)Clustering In Practice
Clustering in Practice
…featuring \(k\)-means
Today we’ll do an extended example showing \(k\)-means clustering in practice and in the context of the python libraries scikit-learn.
scikit-learn is the main python library for machine learning functions.
Our goals are to learn:
- How clustering is used in practice
- Tools for evaluating the quality of a clustering
- Tools for assigning meaning or labels to a cluster
- Important visualizations
- A little bit about feature extraction for text
Visualization
Training wheels: Synthetic data
Generally, when learning about or developing a new unsupervised method, it’s a good idea to try it out on a dataset in which you already know the “right” answer.
One way to do that is to generate synthetic data that has some known properties.
Among other things, scikit-learn contains tools for generating synthetic data for testing.
We’ll use datasets.make_blobs.
Let’s check the shapes of the returned values:
print("X.shape: ", X.shape)
print("y.shape: ", y.shape)
print("gt_centers: ", gt_centers.shape)X.shape: (100, 30)
y.shape: (100,)
gt_centers: (3, 30)datasets.makeblobs takes as arguments:
n_samples: The number of samples to generaten_features: The number of features, or in other words the dimensionality of each samplecenter_box: The bounds of the cluster centersrandom_state: The random seed for reproducibilityreturn_centers: A boolean flag, True to return the centers so that we have ground truth
Visualize the Data
To get a sense of the raw data we can inspect it.
For statistical visualization, a good library is Seaborn.
Let’s plot the X data as a matrix heatmap, where every row is a data point and the columns are the features.
Code
import seaborn as sns
import matplotlib.pyplot as plt
# Set the figure size to make the plot smaller
plt.figure(figsize=(7, 5)) # Adjust the width and height as needed
sns.heatmap(X, xticklabels = False, yticklabels = False, linewidths = 0, cbar = True)
plt.show()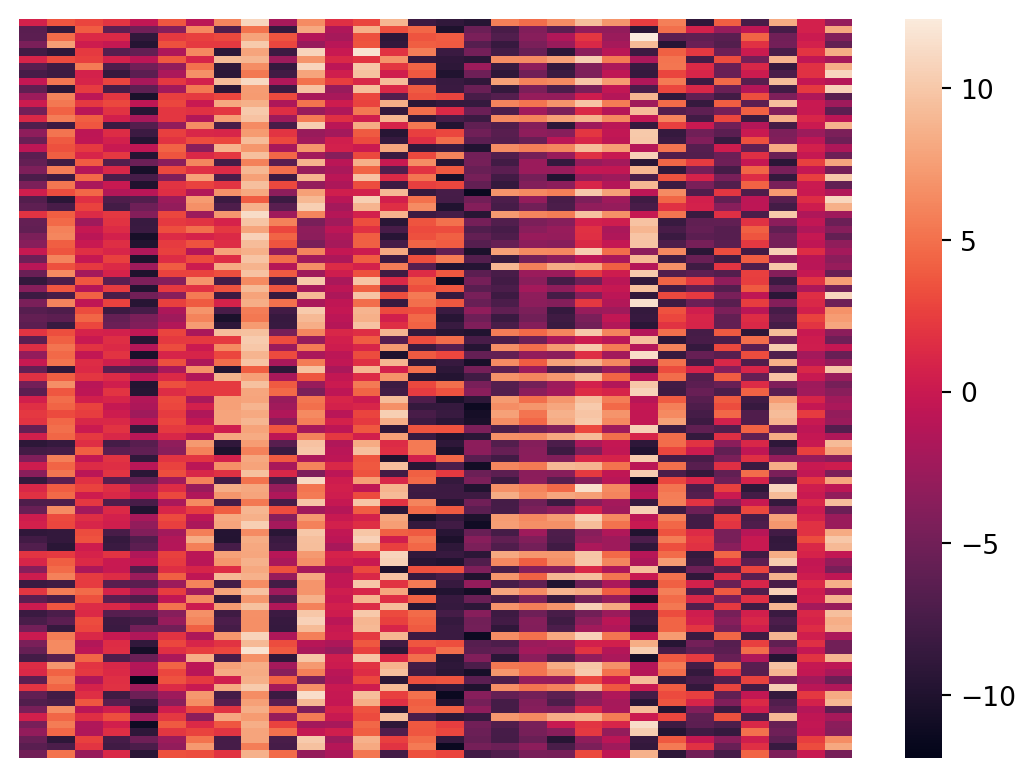
Geometrically, these points live in a 30 dimensional space, so we cannot directly visualize their geometry.
This is a big problem that you will run into time and again!
We will discuss methods for visualizing high dimensional data later on.
For now, we will use a method that can turn a set of pairwise distances into an approximate 2-D representation in some cases.
So let’s compute the pairwise distances, in 30 dimensions, for visualization purposes.
We can compute all pairwise distances in a single step using the scikit-learn metrics.euclidean_distances function:
import sklearn.metrics as metrics
euclidean_dists = metrics.euclidean_distances(X)
# euclidean_dists/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ bMatrix shape is: (100, 100)Let’s look at the upper left and lower right corners of the distances matrix.
Upper left 3x3:
[[ 0. 47.74 45.19]
[47.74 0. 43.67]
[45.19 43.67 0. ]]
...
Lower right 3x3:
[[ 0. 8.19 41.82]
[ 8.19 0. 43.41]
[41.82 43.41 0. ]]/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ bNote that this produces a \(100\times100\) symmetric matrix where the diagonal is all zeros (distance from itself).
Let’s look at a histogram of the distances.
Code
import numpy as np
import matplotlib.pyplot as plt
import sklearn.metrics as metrics
# Compute the pairwise distances
euclidean_dists = metrics.euclidean_distances(X)
# Extract the lower triangular part of the matrix, excluding the diagonal
lower_triangular_values = euclidean_dists[np.tril_indices_from(euclidean_dists, k=-1)]
# Plot the histogram
plt.figure(figsize=(10, 6))
plt.hist(lower_triangular_values, bins=30, edgecolor='black')
plt.title('Histogram of Lower Diagonal Values of Euclidean Distances')
plt.xlabel('Distance')
plt.ylabel('Frequency')
plt.show()/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b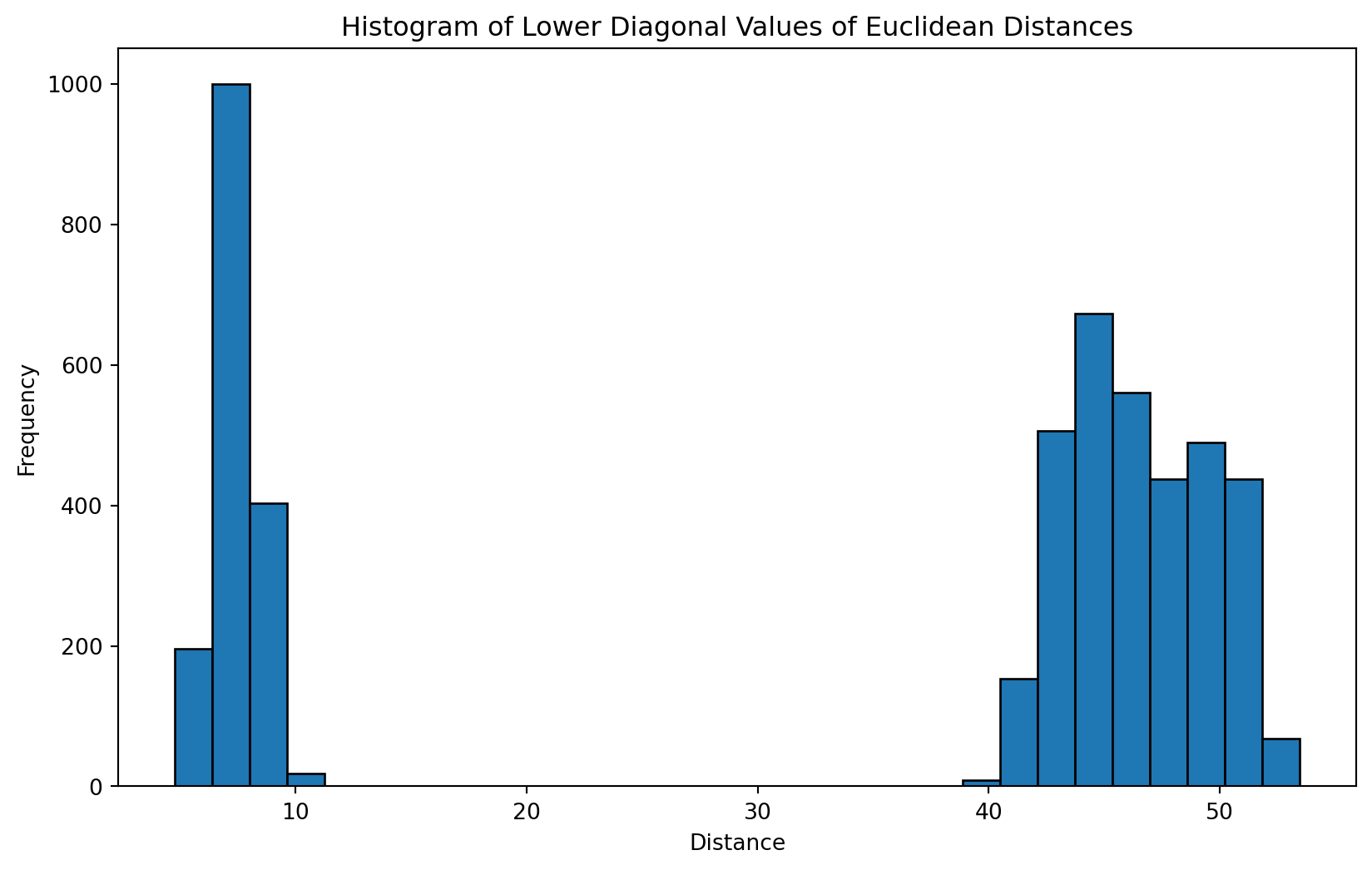
Remember that these are the pairwise distances, in 30 dimensions. So at least with this dataset we see a clean separation presumably between inter-cluster distances and intra-cluster distances.
How would the curse of dimensionality affect this? We discuss the curse of dimensionality later in the course.
Visualizing with MDS
The idea behind Multidimensional Scaling (MDS) is given a pairwise distance (or dissimilarity) matrix:
- Find a set of coordinates in 1, 2 or 3-D space that approximates those distances as well as possible.
- The points that are close (or far) in high dimensional space should be close (or far) in the reduced dimension space.
MDS Continued
Note that there are two forms of MDS:
- Metric MDS, of which Classical MDS is a special case, and has a closed form solution based on the eigenvectors of the centered distance matrix.
- \(O(n^3)\) time complexity and \(O(n^2)\) space complexity.
- Non-Metric MDS, which tries to find a non-parametric monotonic relationship between the dissimilarities and the target coordinates through an iterative approach.
- \(O(n^2)\) time complexity.
Question If non-metric is faster, why not always use it?
Answer: Metric MDS is more faithful to preserving the relative distances between poijnts, where as non-metric MDS preserves the order but not necessarily faithful to the distances.
In general, MDS may not always work well if, for example the dissimilarities are not well modeled by a metric like Euclidean distance.
MDS Visualization Result
Code
import sklearn.manifold
import matplotlib.pyplot as plt
mds = sklearn.manifold.MDS(n_components=2, max_iter=3000, eps=1e-9, random_state=0,
dissimilarity = "precomputed", n_jobs = 1)
fit = mds.fit(euclidean_dists)
pos = fit.embedding_
plt.scatter(pos[:, 0], pos[:, 1], s=8)
plt.axis('square');/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b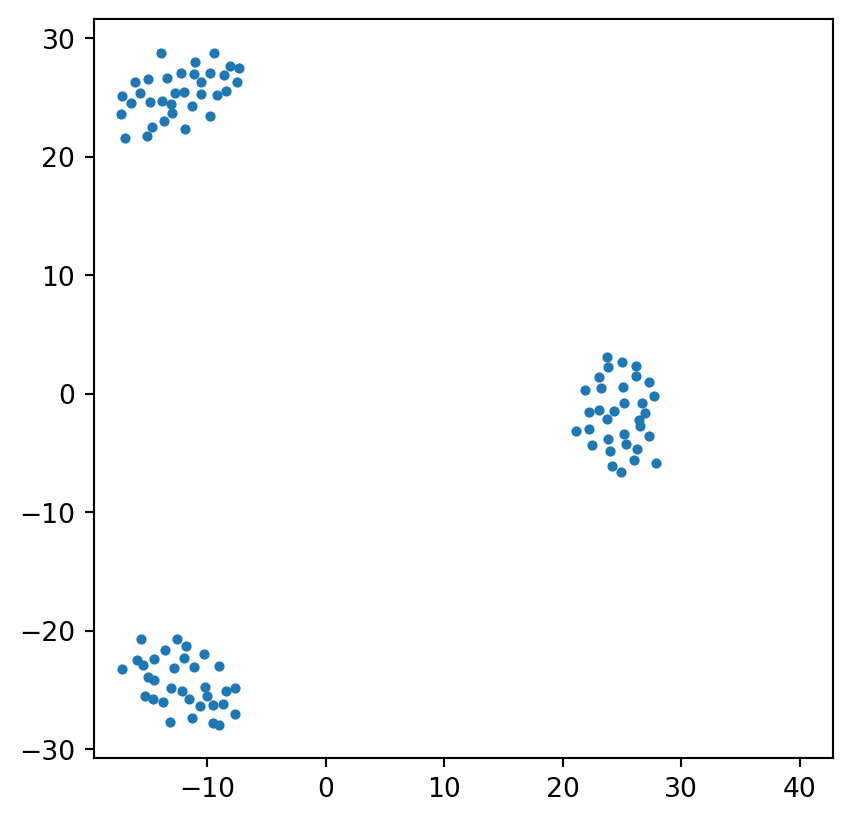
So we can see that, although our data lives in 30 dimensions, we can get a sense of how the points are clustered by approximately placing the points into two dimensions.
Out of curiosity, we can visualize the pairwise distance matrix using a heatmap.
sns.heatmap(euclidean_dists, xticklabels=False, yticklabels=False, linewidths=0,
square=True )
plt.show()
Applying \(k\)-means
Applying \(k\)-Means
The Python package scikit-learn has a huge set of tools for unsupervised learning generally, and clustering specifically.
These are in sklearn.cluster.
There are 3 functions in all the clustering classes,
fit(): builds the model from the training data.- For \(k\)-means, this function find the centroids.
predict(): assigns labels to the data after building the models.- For \(k\)-means this assigns the cluster number to a point.
fit_predict(): calls fit and predict in a single step.
Let’s go back to the original 30-D synthetic dataset and apply \(k\)-means and show the cluster numbers.
Code
from sklearn.cluster import KMeans
kmeans = KMeans(init = 'k-means++', n_clusters = 3, n_init = 100, random_state=0)
y_prime = kmeans.fit_predict(X)
print(y_prime)[0 1 2 2 1 0 1 1 0 1 2 0 2 0 1 2 2 0 2 1 2 1 2 0 1 1 0 2 2 2 2 0 2 0 2 1 2
1 2 1 1 1 0 2 0 2 0 1 0 2 2 0 0 0 0 2 0 1 1 2 0 2 1 0 0 1 2 0 0 1 1 1 0 0
2 0 1 0 1 0 1 1 1 0 2 2 1 0 0 2 0 1 1 2 0 2 2 1 1 2]/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ bFor comparisons, here are the original cluster numbers.
Code
print(y)[0 2 1 1 2 0 2 2 0 2 1 0 1 0 2 1 1 0 1 2 1 2 1 0 2 2 0 1 1 1 1 0 1 0 1 2 1
2 1 2 2 2 0 1 0 1 0 2 0 1 1 0 0 0 0 1 0 2 2 1 0 1 2 0 0 2 1 0 0 2 2 2 0 0
1 0 2 0 2 0 2 2 2 0 1 1 2 0 0 1 0 2 2 1 0 1 1 2 2 1]Note that the \(k\)-means labels are different than the ground truth labels.
We can remap the values according to
\[ \begin{align*} 0 &\rightarrow 0 \\ 1 &\rightarrow 2 \\ 2 &\rightarrow 1. \end{align*} \]
Code
# Remap y_prime
remap = {0: 0, 1: 2, 2: 1}
y_prime_remapped = np.vectorize(remap.get)(y_prime)
print("Remapped y_prime:")
print(y_prime_remapped)Remapped y_prime:
[0 2 1 1 2 0 2 2 0 2 1 0 1 0 2 1 1 0 1 2 1 2 1 0 2 2 0 1 1 1 1 0 1 0 1 2 1
2 1 2 2 2 0 1 0 1 0 2 0 1 1 0 0 0 0 1 0 2 2 1 0 1 2 0 0 2 1 0 0 2 2 2 0 0
1 0 2 0 2 0 2 2 2 0 1 1 2 0 0 1 0 2 2 1 0 1 1 2 2 1]Code
# Calculate the number of mismatched entries
mismatches = np.sum(y != y_prime_remapped)
# Calculate the percentage of mismatched entries
total_entries = len(y)
percentage_mismatched = (mismatches / total_entries) * 100
print(f"Percentage of mismatched entries: {percentage_mismatched:.2f}%")Percentage of mismatched entries: 0.00%To reiterate, mismatches are 0.00%.
All the tools in scikit-learn are implemented as Python objects.
Recall that the general sequence for using a tool from scikit-learn is:
- create the object, probably with some hyperparameter settings or initialization,
- run the method, generally by using the
fit()function, and - examine the results, which are generally property variables of the object.
centroids = kmeans.cluster_centers_
labels = kmeans.labels_
inertia = kmeans.inertia_And we see the resulting cluster inertia.
Code
print(f'Clustering inertia: {inertia:0.1f}.')Clustering inertia: 2733.8.Visualizing the Results of Clustering
Let’s visualize the results. We’ll do that by reordering the data items according to their cluster.
Code
import numpy as np
idx = np.argsort(labels)
rX = X[idx, :]
sns.heatmap(rX, xticklabels = False, yticklabels = False, linewidths = 0)
plt.show()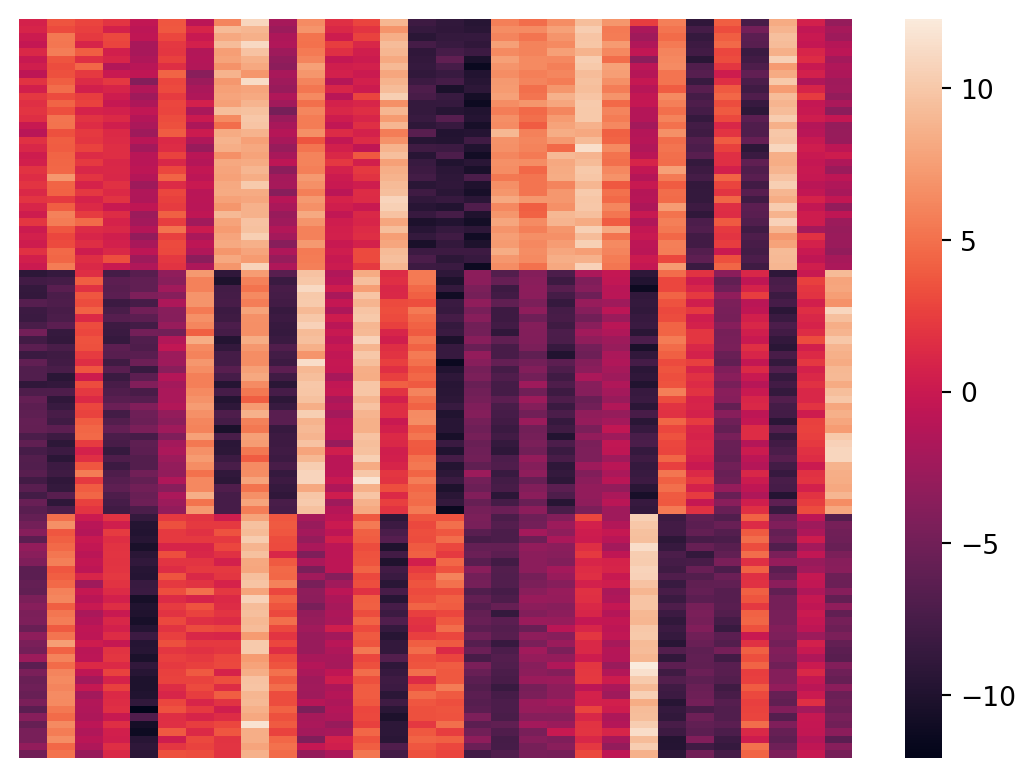
You can clearly see the feature similarities of the samples in the same cluster.
We can also sort the pairwise distance matrix.
Code
rearranged_dists = euclidean_dists[idx,:][:,idx]
sns.heatmap(rearranged_dists, xticklabels = False, yticklabels = False, linewidths = 0, square = True)
plt.show()
Here again, you can see the inter-cluster sample distances are small.
Cluster Evaluation
Cluster Evaluation
How do we know whether the clusters we get represent “real” structure in our data?
Consider a dataset of 100 points uniformly distributed in the unit square.
Question: Does that look uniformly distributed to you?
Code
import pandas as pd
np.random.seed(42)
unif_X = np.random.default_rng().uniform(0, 1, 500)
unif_Y = np.random.default_rng().uniform(0, 1, 500)
df = pd.DataFrame(np.column_stack([unif_X, unif_Y]), columns = ['X', 'Y'])
df.plot('X', 'Y', kind = 'scatter',
colorbar = False, xlim = (0, 1), ylim = (0, 1),
figsize = (4, 4))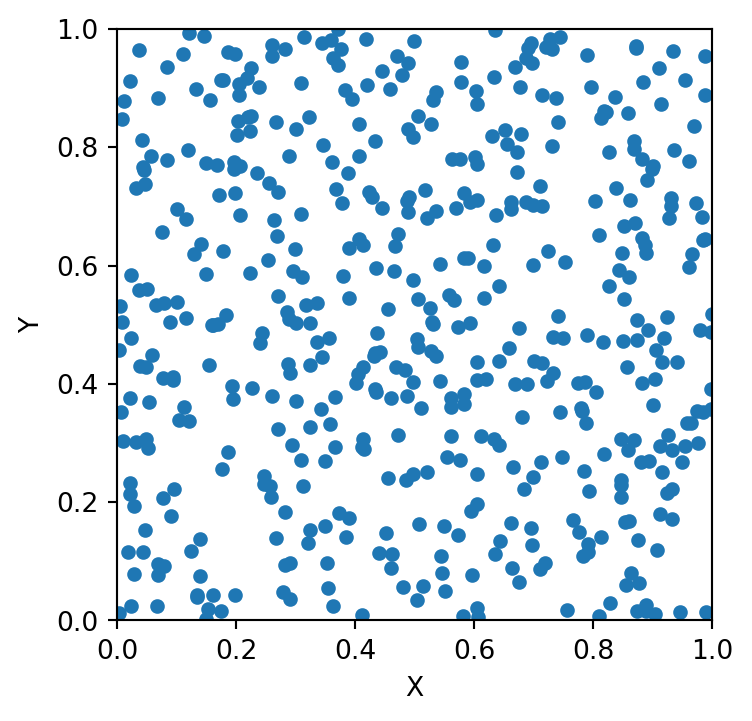
After running \(k\)-means on this data:
Code
kmeans = KMeans(init = 'k-means++', n_clusters = 3, n_init = 500, random_state=0)
df['label'] = kmeans.fit_predict(df[['X', 'Y']])
df.plot('X', 'Y', kind = 'scatter', c = 'label',
colormap='viridis', colorbar = False,
xlim = (0, 1), ylim = (0, 1),
figsize = (4, 4))
The point is: clustering algorithms output some “clustering” of the data.
The question is, does the clustering reflect real structure?
Generally we encounter two problems:
- Are there real clusters in the data?
- If so, how many clusters are there?
There is often no definitive answer to either of these questions.
You will often need to use your judgment in answering them.
Clustering Metrics
Broadly separated into two categories.
- Ground truth based metrics
We’ll look at (Adjusted) Rand Index.
Note: Even with ground truth labels, we can’t apply accuracy measures like we will see in supervised learning approaches since clustering algorithms don’t try to match exact labels, but rather group similar items together.
- Internal cluster metrics (no ground truth external labels)
We’ll look at Silhouette Coefficient.
Rand Index (named after William M. Rand)
- Compare a proposed clustering, \(C\), with ground truth labels, \(T\).
- Look at the ratio, compared to total possible pairs, of pairs of points that are either
- in the same cluster in both \(T\) and \(C\), or
- in different clusters in both \(T\) and \(C\).
Question: What are pairs not in either category?
Rand Index Formula
The formula for the Rand Index is:
\[ \text{RI}(T,C) = \frac{a+b}{n \choose 2}, \]
- where \(a\) is the number of pairs of points that are in the same cluster in both \(T\) and \(C\), and
- \(b\) is the number of pairs of points that are in different clusters in both \(T\) and \(C\).
We normalize the sum by the combinatorial number of pairs of points, \(n \choose 2\).
The Rand Index is a value that falls in the range \([0, 1]\).
Aside: n choose 2
- From combinatorics
“n choose 2” (written as \(n \choose 2\)) represents the number of ways to choose 2 items from a set of n items, where the order doesn’t matter.
Formula
\[ C(n,2) = n! / (2! × (n-2)!) = n(n-1)/2 \]
What it means
- It counts the number of pairs you can form from n items
- Order doesn’t matter (so {A,B} is the same as {B,A})
- No repetition (you can’t choose the same item twice)
Examples
- 3 choose 2: From items {A, B, C}, you can form pairs {A,B}, {A,C}, {B,C} = 3 pairs
- 4 choose 2: From items {A, B, C, D}, you can form pairs {A,B}, {A,C}, {A,D}, {B,C}, {B,D}, {C,D} = 6 pairs
- 5 choose 2: From items {A, B, C, D, E}, you can form 10 pairs
Rand Index Example 1
Let’s proceed by way of example.
We’ll create another synthetic dataset of 3 clusters, so we have ground truth labels \(T\).
X_rand, y_rand = sk_data.make_blobs(n_samples=[100, 300, 50],
centers = [[1.2, 2.4],[1.5, 3], [1.8, 3.5]],
n_features = 2,
center_box = (-10.0, 10.0),
cluster_std = [.2, .3, .2],
random_state = 0)
df_rand_gt = pd.DataFrame(np.column_stack([X_rand[:, 0], X_rand[:, 1], y_rand]), columns = ['X', 'Y', 'label'])
df_rand_clust = df_rand_gt.copy()
kmeans = KMeans(init = 'k-means++', n_clusters = 3, n_init = 100, random_state=0)
df_rand_clust['label'] = kmeans.fit_predict(df_rand_gt[['X', 'Y']])
df_rand_clust['label'] = df_rand_clust['label'].replace({0: 1, 1: 2, 2: 0})Rand Index Example 1: Plotting the Results
We then run \(k\)-means with 3 clusters to on the datasets to get labels \(C\) and plot the results:
Code
figs, axs = plt.subplots(1, 2, figsize = (12, 5))
df_rand_gt.plot('X', 'Y',
kind = 'scatter',
c = 'label',
colormap='viridis',
ax = axs[0],
colorbar = False)
axs[0].set_title('Ground Truth (T)')
axs[0].set_axis_off()
df_rand_clust.plot('X', 'Y',
kind = 'scatter',
c = 'label',
colormap='viridis',
ax = axs[1],
colorbar = False)
axs[1].set_title('Clustering (C)')
axs[1].set_axis_off()
plt.show()
Code
print("The Rand index is: ", metrics.rand_score(df_rand_gt["label"], df_rand_clust["label"]))The Rand index is: 0.5814798317248205Adjusted Rand Index
How do we know whether a particular Rand Index (RI) score is significant?
We might compare it to the RI for a random assignment of points to labels.
This leads to the Adjusted Rand Index.
The Adjusted Rand Index
To calibrate the Rand Index this way, we use the expected Rand Index of random labels, denoted \(E[\text{RI}]\).
The Expected Rand Index considers \(C\) to be a clustering that has the same cluster sizes as \(T\), but the labels are assigned at random.
Using that, we define the adjusted Rand index as a simple rescaling of RI:
\[ \text{ARI} = \frac{\text{RI} - E[\text{RI}]}{1 - E[\text{RI}]} \]
Where \(1\) represents \(\max(\text{RI})\), the maximum possible Rand Index.
\(E[\text{RI}]\) can be computed using combinatorics (we’ll omit the derivation).
The below code block computes and prints the adjusted Rand index for the example on the previous slide.
Code
print("The adjusted Rand index is: ", metrics.adjusted_rand_score(df_rand_gt["label"], df_rand_clust["label"]))The adjusted Rand index is: 0.16578149408651535Rand Index Example 2
Let’s consider again our 3-cluster dataset with known labels y.
Code
import matplotlib.pyplot as plt
plt.figure(figsize=(5, 4)) # Adjust the width and height as needed
sns.heatmap(X, xticklabels = False, yticklabels = False, linewidths = 0)
plt.show()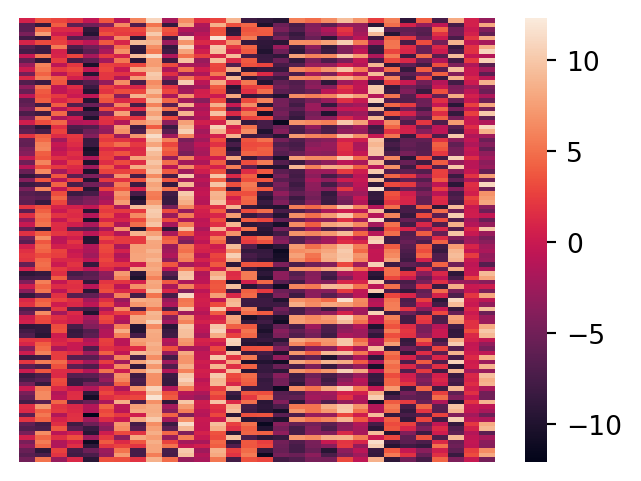
Rand Index Example 2: Evaluating the Results
Here is the Rand Index and adjusted Rand Index, when using \(k\)-means to cluster this dataset for 1 to 10 clusters:
Code
def ri_evaluate_clusters(X, max_clusters, ground_truth):
ri = np.zeros(max_clusters+1)
ri[0] = 0
ari = np.zeros(max_clusters+1)
ari[0] = 0
for k in range(1,max_clusters+1):
kmeans = KMeans(init='k-means++', n_clusters=k, n_init=10)
kmeans.fit_predict(X)
ri[k] = metrics.rand_score(kmeans.labels_, ground_truth)
ari[k] = metrics.adjusted_rand_score(kmeans.labels_, ground_truth)
return ri, ari
ri, ari = ri_evaluate_clusters(X, 10, y)
plt.figure(figsize=(6, 4))
plt.plot(range(1, len(ri)), ri[1:], 'ro-', range(1, len(ari)), ari[1:], 'b*-')
plt.xlabel('Number of clusters')
plt.title('$k$-means Clustering Compared to Known Labels')
plt.ylabel('Index value')
plt.legend(['RI', 'ARI'])
plt.show()/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b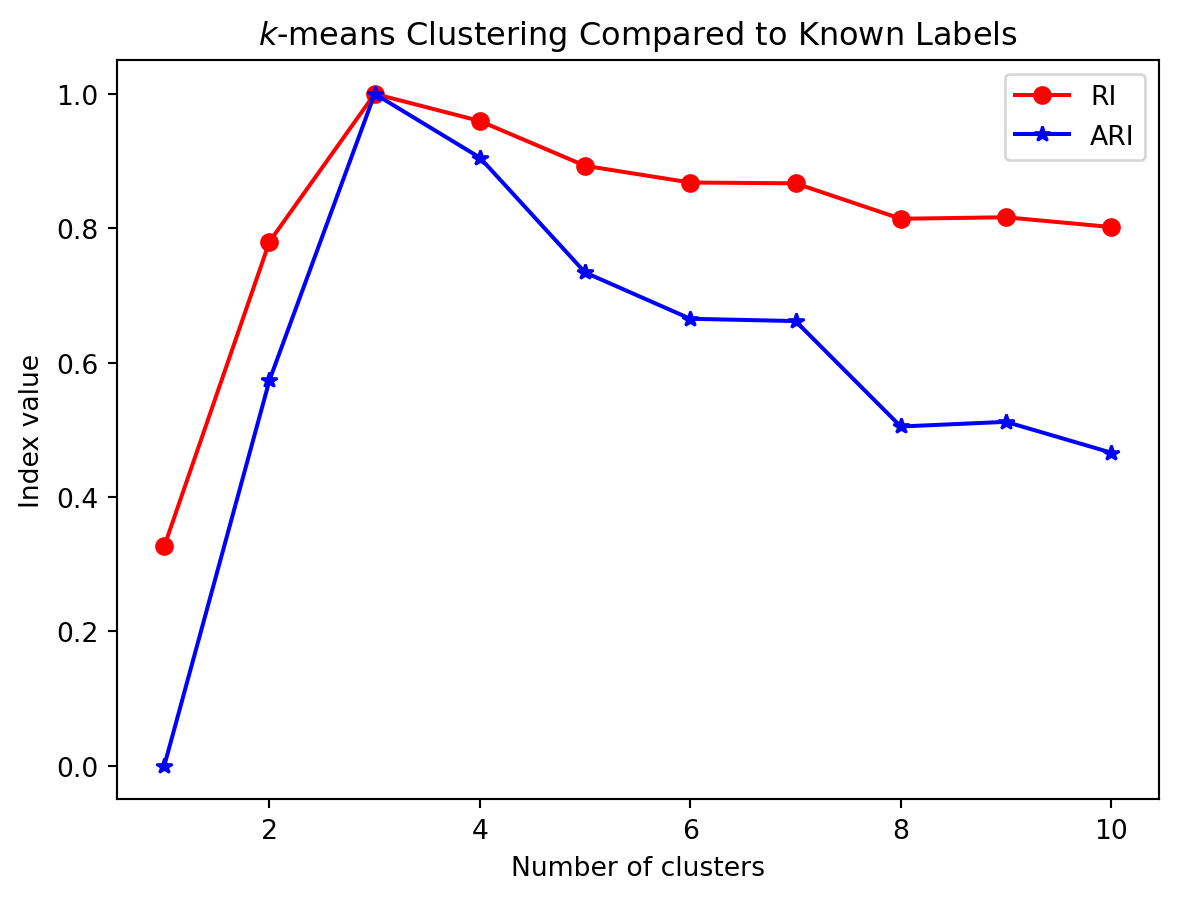
RI vs ARI
The ARI provides a more nuanced evaluation of clustering similarity compared to the RI by accounting for the chance grouping of elements. Here are the key differences:
Rand Index (RI)
- Measures Agreement: The RI measures the agreement between two clusterings by considering all pairs of elements and counting pairs that are either in the same or different clusters in both clusterings.
- Range: The RI ranges from 0 to 1, where 1 indicates perfect agreement and 0 indicates no agreement.
Adjusted Rand Index (ARI)
- Adjusts for Chance: The ARI adjusts the RI by considering the expected similarity that might occur by random chance. This adjustment makes the ARI a more reliable measure, especially when dealing with random or unbalanced clusterings.
- Range: The ARI can take values from -1 to 1. A value of 0 indicates that the clustering is no better than random, while a value of 1 indicates perfect agreement. Negative values indicate that the clustering is worse than random.
Information Provided by ARI
The ARI corrects for the fact that some level of agreement between clusterings can occur purely by chance. This makes it a more accurate measure of the true similarity between clusterings.
The ARI’s range allows for a clearer interpretation of clustering performance. An ARI of 0 means the clustering is no better than random, which is more informative than an RI of 0.5, which might still be influenced by chance.
The ARI allows for better comparison between different clustering results, as it normalizes the index to account for the chance agreement.
Deciding on the Number of Clusters
The second question we face in evaluating a clustering is how many clusters are present.
In practice, to use \(k\)-means or most other clustering methods, one must choose \(k\), the number of clusters, via some process.
Inspecting Clustering Error
The first thing you might do is to look at the \(k\)-means objective function and see if it levels off after a certain point.
Recall that the \(k\)-means objective can be considered the clustering “error”.
If the error stops going down, that would suggest that the clustering is not improving as the number of clusters is increased.
Let’s calculate the error for 1-11 clusters.
error = np.zeros(11)
for k in range(1,11):
kmeans = KMeans(init='k-means++', n_clusters = k, n_init = 10)
kmeans.fit_predict(X)
error[k] = kmeans.inertia_/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ bFor our synthetic data, here is the \(k\)-means objective, as a function of \(k\):
Code
plt.plot(range(1, len(error)), error[1:], 'o-')
plt.xlabel('Number of clusters')
plt.title(r'$k$-means clustering performance of synthetic data')
plt.ylabel('Error')
plt.show()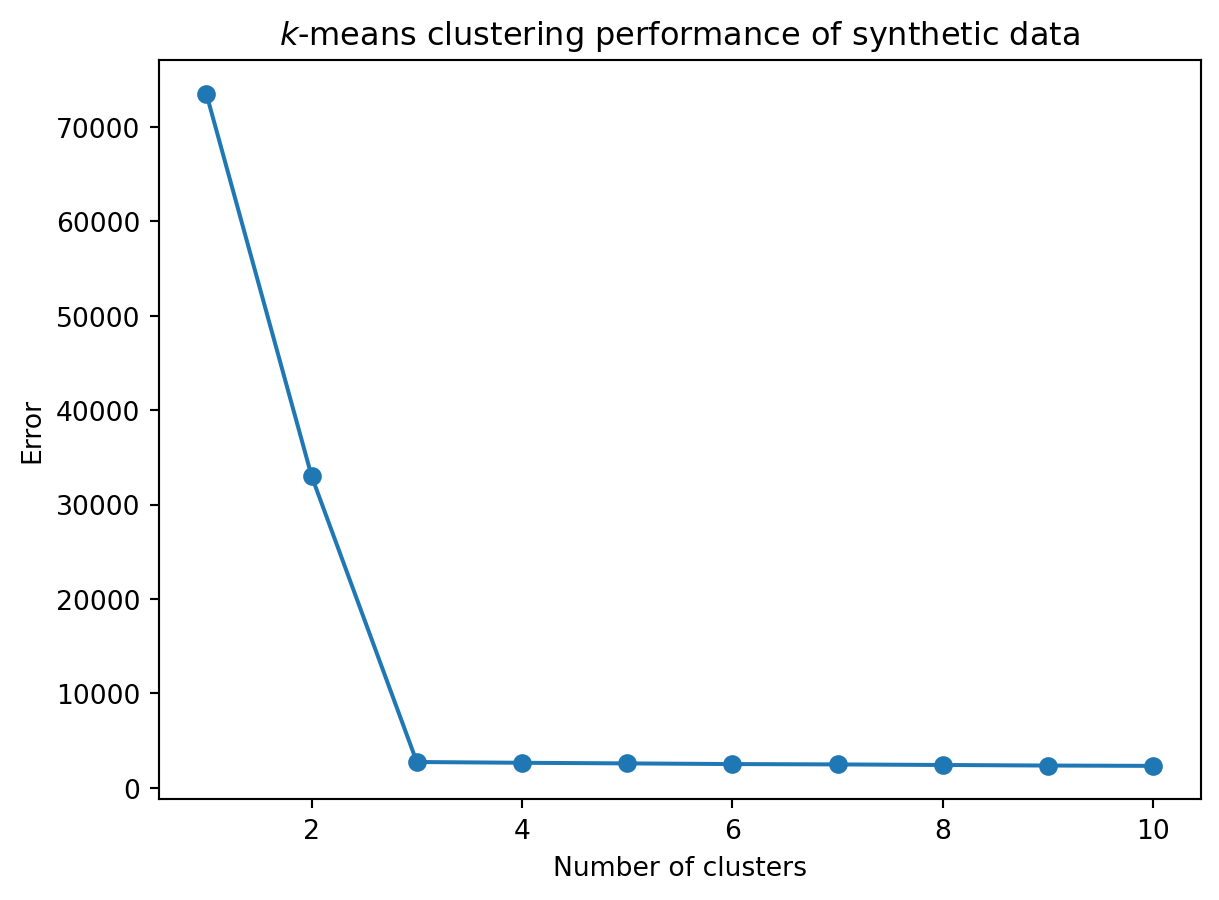
This synthetic data is not at all typical. You will almost never see such a sharp change in the error function as we see here.
Let’s create a function to evaluate clusters for later use.
def evaluate_clusters(X,max_clusters):
error = np.zeros(max_clusters+1)
error[0] = 0
for k in range(1,max_clusters+1):
kmeans = KMeans(init='k-means++', n_clusters=k, n_init=10)
kmeans.fit_predict(X)
error[k] = kmeans.inertia_
return errorSilhouette Coefficient
Usually, the ground truth labels are not known.
In that case, evaluation must be performed using the model itself.
Recall our definition of clustering:
a grouping of data objects, such that the objects within a group are similar (or near) to one another and dissimilar (or far) from the objects in other groups.
This suggests a metric that could evaluate a clustering: comparing the distances between points within a cluster, to the distances between points in different clusters.
Silhouette Coefficient
The Silhouette Coefficient is an example of such an evaluation, where a higher Silhouette Coefficient score relates to a model with “better defined” clusters. We’ll use sklearn.metrics.silhouette_score
- Let \(a\) be the mean distance between a data point and all other points in the same cluster.
- Let \(b\) be the mean distance between a data point and all other points in the next nearest cluster.
Then the Silhouette Coefficient for a point is
\[ s = \frac{b-a}{\max(a, b)}. \]
where \(\max(a, b)\) is the larger of the two mean distances.
Why This Makes Sense
The max(a, b) normalization ensures the coefficient is always between -1 and 1:
- If a < b (good clustering): Point is closer to its own cluster
- max(a, b) = b
- s = (b - a) / b = 1 - (a/b) → positive (0 to 1)
- If a > b (poor clustering): Point is closer to other clusters
- max(a, b) = a
- s = (b - a) / a = (b/a) - 1 → negative (-1 to 0)
- If a = b (boundary): Point is equidistant
- s = 0
This creates a scale where:
- +1 = perfectly clustered (a = 0, b > 0)
- 0 = on the boundary (a = b)
- -1 = completely misclustered (b = 0, a > 0)
Overall Silhouette Score
The overall silhouette score is the average of the silhouette coefficient for each data point.
\[ (1/n) \sum_{i=1}^n s_i \]
Silhouette Score for our synthetic data
We can calculate the Silhouette Score for our synthetic data:
Code
sc = metrics.silhouette_score(X, labels, metric='euclidean')
print('Silhouette Score:', sc)Silhouette Score: 0.8319348841402534/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ bWe can also evaluate it for 2-10 clusters and plot the results:
Code
def sc_evaluate_clusters(X, max_clusters, n_init, seed):
s = np.zeros(max_clusters+1)
s[0] = 0
s[1] = 0
for k in range(2, max_clusters+1):
kmeans = KMeans(init='k-means++', n_clusters = k, n_init = n_init, random_state = seed)
kmeans.fit_predict(X)
s[k] = metrics.silhouette_score(X, kmeans.labels_, metric = 'euclidean')
return s
s = sc_evaluate_clusters(X, 10, 10, 1)
plt.plot(range(2, len(s)), s[2:], 'o-')
plt.xlabel('Number of Clusters')
plt.title('$k$-means clustering performance on synthetic data')
plt.ylabel('Silhouette Score')
plt.show()/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b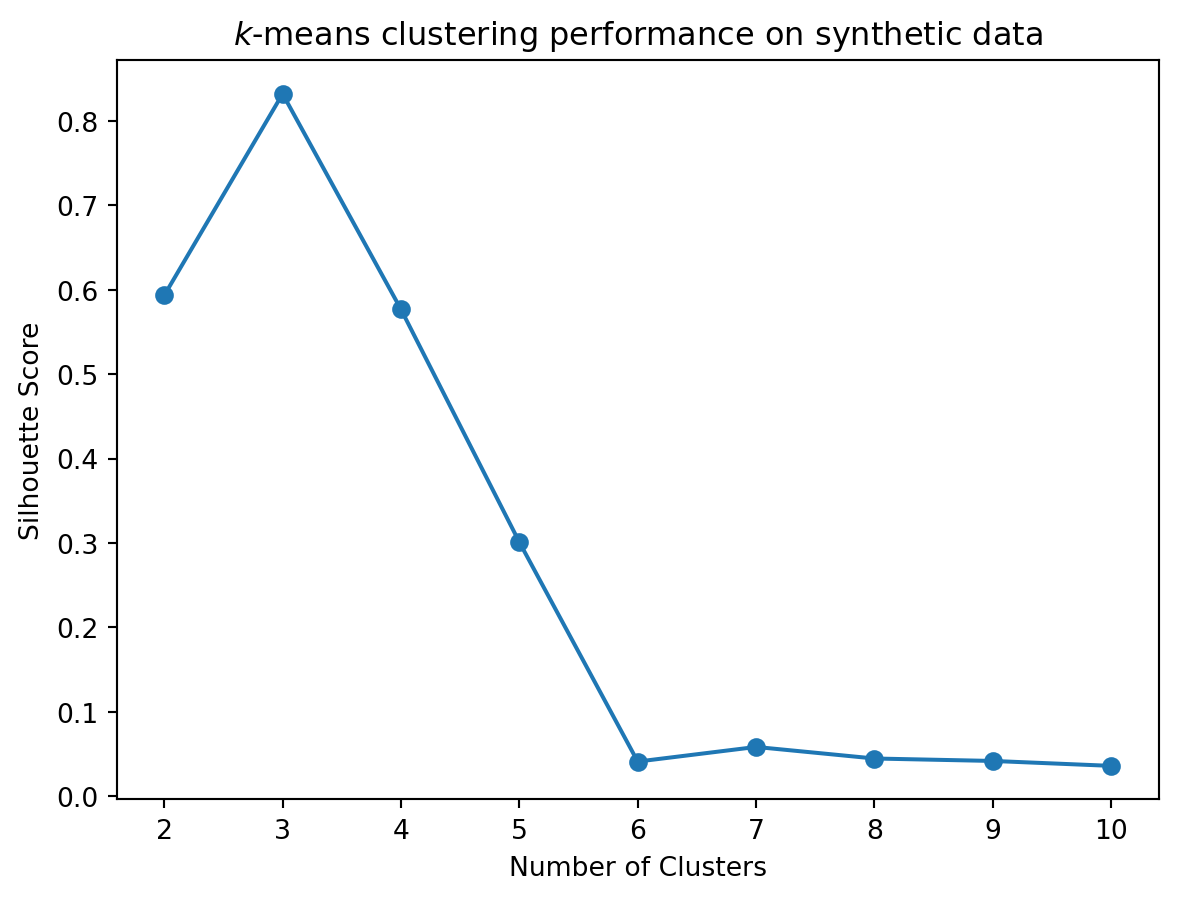
Again, these results are more perfect than typical.
But the general idea is to look for a local maximum in the Silhouette Coefficient as the potential number of clusters.
k-means++
k-means++ initialization
Proposed in 2007 by David Arthur and Sergei Vassilvitskii.
K-means++ improves the initialization of cluster centers to enhance the quality of the final clustering results. Here’s how it works.
- Choose an initial centroid \(c_1\) randomly.
- Choose the next centroid \(c_i\) with probability proportional to the squared distances to each data point.
- This ensures that new centroids are spread out across the data space.
- Repeat this process until \(k\) centroids have been selected.
Once the initial centroids are chosen, the standard k-means algorithm is applied.
The main advantage of k-means++ over randomly assigning points is that it reduces the likelihood of poor clustering results due to suboptimal initial centroids. This often leads to faster convergence and better overall clustering quality.
Visualizing K-means++ Initialization Probability
Let’s create a visualization that demonstrates how K-means++ selects the second centroid based on the squared distances from the first selected point:
Code
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
# Create a small uniformly distributed 2D dataset
np.random.seed(42)
n_points = 100
X = np.random.uniform(-5, 5, (n_points, 2))
# Select the first centroid randomly (simulate k-means++ first step)
first_centroid = X[0] # For demonstration, we'll use the first point
# Calculate squared distances from all points to the first centroid
distances_squared = np.sum((X - first_centroid)**2, axis=1)
# Normalize to get probabilities (proportional to squared distances)
probabilities = distances_squared / np.sum(distances_squared)
# Create 3D plot
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
# Plot the 2D points
ax.scatter(X[:, 0], X[:, 1], c='lightblue', s=30, alpha=0.6, label='Data points')
# Highlight the first centroid
ax.scatter(first_centroid[0], first_centroid[1], c='red', s=100, marker='*',
label='First centroid', edgecolors='darkred', linewidth=2)
# Create 3D visualization where z-axis represents probability
# We'll create a grid to show the probability surface
x_range = np.linspace(X[:, 0].min(), X[:, 0].max(), 50)
y_range = np.linspace(X[:, 1].min(), X[:, 1].max(), 50)
X_grid, Y_grid = np.meshgrid(x_range, y_range)
# Calculate probability for each grid point
grid_distances_squared = (X_grid - first_centroid[0])**2 + (Y_grid - first_centroid[1])**2
grid_probabilities = grid_distances_squared / np.sum(grid_distances_squared)
# Plot the probability surface
surf = ax.plot_surface(X_grid, Y_grid, grid_probabilities,
alpha=0.3, cmap='viridis',
linewidth=0, antialiased=True)
# Add the actual data points with their probabilities as z-values
ax.scatter(X[:, 0], X[:, 1], probabilities, c='darkblue', s=20, alpha=0.8)
# Add colorbar
fig.colorbar(surf, ax=ax, shrink=0.5, aspect=20, label='Selection Probability')
# Set labels and title
ax.set_xlabel('X coordinate')
ax.set_ylabel('Y coordinate')
ax.set_zlabel('Selection Probability')
ax.set_title('K-means++ Initialization Probability\n(Probability ∝ Squared Distance from First Centroid)')
# Add legend
ax.legend()
# Set viewing angle for better visualization
ax.view_init(elev=20, azim=45)
plt.tight_layout()
plt.show()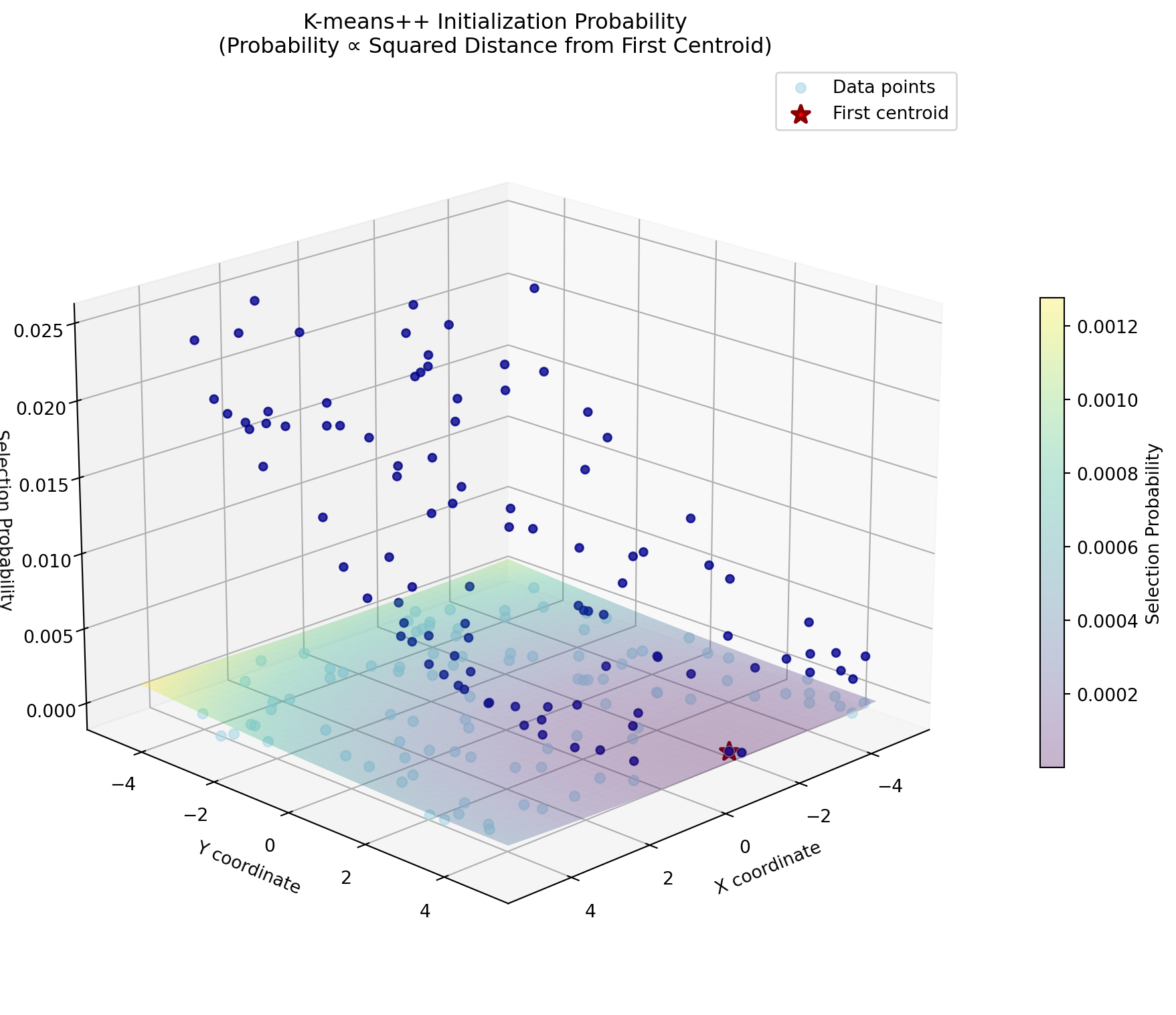
This 3D visualization shows:
- Light Blue points: The uniformly distributed 2D dataset
- Red star: The first randomly selected centroid
- Surface and Dark Blue points: The probability of selecting each point as the second centroid
- Z-axis: Represents the selection probability (proportional to squared distance from first centroid)
As you can see, points farther from the first centroid have higher selection probability, which helps ensure that the second centroid is well-separated from the first one.
Real Data Clustering Example
Taking the Training Wheels Off: Real Data
As a classic “real world” example, we’ll use the “20 Newsgroup” data provided as example data in scikit-learn.
We borrow code from this sklearn example.
Let’s load the data and count the number of documents and categories.
from sklearn.datasets import fetch_20newsgroups
# just use the following categories
categories = ['comp.os.ms-windows.misc', 'sci.space', 'rec.sport.baseball']
news_data = fetch_20newsgroups(
remove = ('headers', 'footers', 'quotes'),
subset = 'train',
categories = categories,
shuffle = True,
random_state = 42)
labels = news_data.target
unique_labels, category_sizes = np.unique(labels, return_counts=True)
true_k = unique_labels.shape[0]
print(f"{len(news_data.data)} documents - {true_k} categories")1781 documents - 3 categoriesExample Document
Here is an example of one of the documents:
Code
print(news_data.data[0])
Early to mid June.
If they think the public wants to see it they will carry it. Why not
write them and ask? You can reach them at:
F: NATIONAL NEWS MEDIA
ABC "World News Tonight" "Face the Nation"
7 West 66th Street CBS News
New York, NY 10023 2020 M Street, NW
212/887-4040 Washington, DC 20036
202/457-4321
Associated Press "Good Morning America"
50 Rockefeller Plaza ABC News
New York, NY 10020 1965 Broadway
National Desk (212/621-1600) New York, NY 10023
Foreign Desk (212/621-1663) 212/496-4800
Washington Bureau (202/828-6400)
Larry King Live TV
"CBS Evening News" CNN
524 W. 57th Street 111 Massachusetts Avenue, NW
New York, NY 10019 Washington, DC 20001
212/975-3693 202/898-7900
"CBS This Morning" Larry King Show--Radio
524 W. 57th Street Mutual Broadcasting
New York, NY 10019 1755 So. Jefferson Davis Highway
212/975-2824 Arlington, VA 22202
703/685-2175
"Christian Science Monitor"
CSM Publishing Society "Los Angeles Times"
One Norway Street Times-Mirror Square
Boston, MA 02115 Los Angeles, CA 90053
800/225-7090 800/528-4637
CNN "MacNeil/Lehrer NewsHour"
One CNN Center P.O. Box 2626
Box 105366 Washington, DC 20013
Atlanta, GA 30348 703/998-2870
404/827-1500
"MacNeil/Lehrer NewsHour"
CNN WNET-TV
Washington Bureau 356 W. 58th Street
111 Massachusetts Avenue, NW New York, NY 10019
Washington, DC 20001 212/560-3113
202/898-7900
"Crossfire" NBC News
CNN 4001 Nebraska Avenue, NW
111 Massachusetts Avenue, NW Washington, DC 20036
Washington, DC 20001 202/885-4200
202/898-7951 202/362-2009 (fax)
"Morning Edition/All Things Considered"
National Public Radio
2025 M Street, NW
Washington, DC 20036
202/822-2000
United Press International
1400 Eye Street, NW
Washington, DC 20006
202/898-8000
"New York Times" "U.S. News & World Report"
229 W. 43rd Street 2400 N Street, NW
New York, NY 10036 Washington, DC 20037
212/556-1234 202/955-2000
212/556-7415
"New York Times" "USA Today"
Washington Bureau 1000 Wilson Boulevard
1627 Eye Street, NW, 7th Floor Arlington, VA 22229
Washington, DC 20006 703/276-3400
202/862-0300
"Newsweek" "Wall Street Journal"
444 Madison Avenue 200 Liberty Street
New York, NY 10022 New York, NY 10281
212/350-4000 212/416-2000
"Nightline" "Washington Post"
ABC News 1150 15th Street, NW
47 W. 66th Street Washington, DC 20071
New York, NY 10023 202/344-6000
212/887-4995
"Nightline" "Washington Week In Review"
Ted Koppel WETA-TV
ABC News P.O. Box 2626
1717 DeSales, NW Washington, DC 20013
Washington, DC 20036 703/998-2626
202/887-7364
"This Week With David Brinkley"
ABC News
1717 DeSales, NW
Washington, DC 20036
202/887-7777
"Time" magazine
Time Warner, Inc.
Time & Life Building
Rockefeller Center
New York, NY 10020
212/522-1212
Feature Extraction
We’ve discussed a bit the challenges of feature engineering.
One of the most basic issues concerns how to encode categorical or text data in a form usable by algorithms that expect numeric input.
The starting point is to note that one can encode a set using a binary vector with one component for each potential set member.
Bag of Words
The so-called bag of words encoding for a document is to treat the document as a multiset of words.
A multiset is like a set but allows for multiple instances of each element.
That is, we simply count how many times each word occurs. It is a “bag” because all the order of the words in the document is lost.
Surprisingly, we can still tell a lot about the document even without knowing its word ordering.
Bag of Words Example
Consider this short document (one paragraph):
“The quick brown fox jumps over the lazy dog. The dog sleeps soundly at noon.”
We ignore word order and count occurrences of each word.
import re
from collections import Counter
doc = (
"The quick brown fox jumps over the lazy dog. "
"The dog sleeps soundly at noon."
)
# simple tokenization: lowercase and keep alphabetic words
tokens = re.findall(r"[a-zA-Z']+", doc.lower())
counts = Counter(tokens)
# show vocabulary and frequencies sorted by word
sorted_counts = sorted(counts.items())
sorted_counts[('at', 1),
('brown', 1),
('dog', 2),
('fox', 1),
('jumps', 1),
('lazy', 1),
('noon', 1),
('over', 1),
('quick', 1),
('sleeps', 1),
('soundly', 1),
('the', 3)]You can also view the words and counts as separate vectors:
Code
vocabulary = [w for w, c in sorted_counts]
frequencies = [c for w, c in sorted_counts]
print('words =', vocabulary)
print('counts =', frequencies)words = ['at', 'brown', 'dog', 'fox', 'jumps', 'lazy', 'noon', 'over', 'quick', 'sleeps', 'soundly', 'the']
counts = [1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 3]Term Frequencies
Counting the number of times each word occurs in a document yields a vector of term frequencies.
However, simply using the “bag of words” directly has a number of drawbacks. First of all, large documents will have more words than small documents.
Hence it often makes sense to normalize the frequency vectors.
\(\ell_1\) or \(\ell_2\) normalization are common.
Bag of Words: Normalization
We can scale raw counts so documents of different lengths are comparable.
Code
import math
try:
sorted_counts # reuse if already defined above
except NameError:
import re
from collections import Counter
doc = (
"The quick brown fox jumps over the lazy dog. "
"The dog sleeps soundly at noon."
)
tokens = re.findall(r"[a-zA-Z']+", doc.lower())
from collections import Counter
counts = Counter(tokens)
sorted_counts = sorted(counts.items())
vocabulary = [w for w, c in sorted_counts]
counts_vec = [c for w, c in sorted_counts]
# L1 normalization: divide by sum of counts
total = sum(counts_vec)
l1 = [c / total for c in counts_vec]
# L2 normalization: divide by Euclidean norm
norm2 = math.sqrt(sum(c*c for c in counts_vec))
l2 = [c / norm2 for c in counts_vec]
print('words =', vocabulary)
print('\nL1-normalized counts =', [f'{x:.2f}' for x in l1])
print(f"Sum of L1-normalized counts = {sum(l1):.2f}")
print('\nL2-normalized counts =', [f'{x:.2f}' for x in l2])
print(f"Sum of L2-normalized counts = {sum(l2):.2f}")
norm2norm = math.sqrt(sum(c*c for c in l2))
print(f"The L2 norm of L2-normalized counts = {norm2norm:.2f}")words = ['at', 'brown', 'dog', 'fox', 'jumps', 'lazy', 'noon', 'over', 'quick', 'sleeps', 'soundly', 'the']
L1-normalized counts = ['0.07', '0.07', '0.13', '0.07', '0.07', '0.07', '0.07', '0.07', '0.07', '0.07', '0.07', '0.20']
Sum of L1-normalized counts = 1.00
L2-normalized counts = ['0.21', '0.21', '0.42', '0.21', '0.21', '0.21', '0.21', '0.21', '0.21', '0.21', '0.21', '0.63']
Sum of L2-normalized counts = 3.13
The L2 norm of L2-normalized counts = 1.00Tf-idf
Next, as noted in scikit-learn:
- In a large text corpus, some words will be very frequent (e.g. “the”, “a”, “is” in English) hence carrying very little meaningful information about the actual contents of the document.
- If we were to feed the direct count data directly to a classifier those very frequent terms would overshadow the frequencies of rarer yet more interesting terms.
- In order to re-weight the count features into floating point values suitable for usage by a classifier it is very common to use the tf–idf transform.
- Tf means term-frequency while tf–idf means term-frequency times inverse document-frequency.
- This is originally a term weighting scheme developed for information retrieval (as a ranking function for search engines results), that has also found good use in document classification and clustering.
The idea is that rare words are more informative than common words.
(This has connections to information theory).
Tf-idf Definition
Hence, the definition of tf-idf is as follows.
First:
\[ \text{tf}(t,d) = \text{Number of times term }t \text{ occurs in document } d~. \]
Next, if \(N\) is the total number of documents in the corpus \(D\) then:
\[ \text{idf}(t,D)=\log{\frac{N}{|\{d\in D : t\in d \}|}}, \]
where the denominator is the number of documents in which the term \(t\) appears.
And finally:
\[ \text{tf-idf}(t,d)=\text{tf}(t,d)\times \text{idf}(t,D). \]
Code
from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer(stop_words = 'english', min_df = 4, max_df = 0.8)
data = vectorizer.fit_transform(news_data.data)TF-IDF on Newsgroup Data
Code
from sklearn.feature_extraction.text import TfidfVectorizer
import numpy as np
# Reuse previously loaded 20 Newsgroups subset if available; otherwise load it
try:
news_data
categories
except NameError:
from sklearn.datasets import fetch_20newsgroups
categories = ['comp.os.ms-windows.misc', 'sci.space', 'rec.sport.baseball']
news_data = fetch_20newsgroups(
remove=('headers', 'footers', 'quotes'),
subset='train',
categories=categories,
shuffle=True,
random_state=42,
)
# pick one example document from each category
docs_by_cat = []
labels = news_data.target
for cat_index in range(len(categories)):
# first document whose label matches the category index
indices = np.where(labels == cat_index)[0]
if len(indices) > 0:
docs_by_cat.append(news_data.data[indices[0]])
# compute TF-IDF on the selected three documents
tfidf_vec = TfidfVectorizer(stop_words='english', min_df=1, max_df=1.0)
X = tfidf_vec.fit_transform(docs_by_cat)
feature_names = np.array(tfidf_vec.get_feature_names_out())
def top_terms(row_vector, k=10):
row = row_vector.toarray().ravel()
if row.sum() == 0:
return []
top_idx = np.argsort(row)[-k:][::-1]
return list(zip(feature_names[top_idx], row[top_idx]))
for i, doc in enumerate(docs_by_cat):
print(f"\nDocument {i+1} (category: {categories[i]}): Top TF-IDF terms")
for term, score in top_terms(X[i], k=10):
print(f" {term:20s} {score:.4f}")
print(f"The shape of the TF-IDF matrix is {X.shape}")
Document 1 (category: comp.os.ms-windows.misc): Top TF-IDF terms
problem 0.2597
remember 0.2597
win31 0.2597
computer 0.2597
dos 0.2597
time 0.1975
stacker 0.1298
prompt 0.1298
defragmented 0.1298
thank 0.1298
Document 2 (category: sci.space): Top TF-IDF terms
good 0.3150
canadian 0.2071
valentine 0.2071
nothin 0.2071
old 0.2071
logic 0.2071
like 0.2071
rings 0.2071
rotation 0.2071
say 0.2071
Document 3 (category: rec.sport.baseball): Top TF-IDF terms
washington 0.3863
street 0.3050
202 0.2847
dc 0.2847
york 0.2643
212 0.2643
new 0.2643
nw 0.2440
ny 0.2237
news 0.2033
The shape of the TF-IDF matrix is (3, 279)Getting to know the Data
Code
print(f'The datas type is {type(data)} and the shape is {data.shape}')The datas type is <class 'scipy.sparse._csr.csr_matrix'> and the shape is (1781, 6613)For what it’s worth we can look at the data feature matrix:
Code
fig, ax1 = plt.subplots(1,1,figsize=(8,4))
dum = sns.heatmap(data[1:100,1:200].todense(), xticklabels=False, yticklabels=False,
linewidths=0, cbar=True, ax=ax1)
Code
print(news_data.target)
print(news_data.target_names)[2 0 0 ... 2 1 2]
['comp.os.ms-windows.misc', 'rec.sport.baseball', 'sci.space']Selecting the Number of Clusters – Error
Now let’s look at the different cluster measures versus number of clusters.
Code
error = evaluate_clusters(data, 10)
plt.plot(range(1, len(error)), error[1:])
plt.title('$k$-means Clustering Performance on Newsgroup Articles')
plt.xlabel('Number of clusters')
plt.ylabel('Error')
plt.show()/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight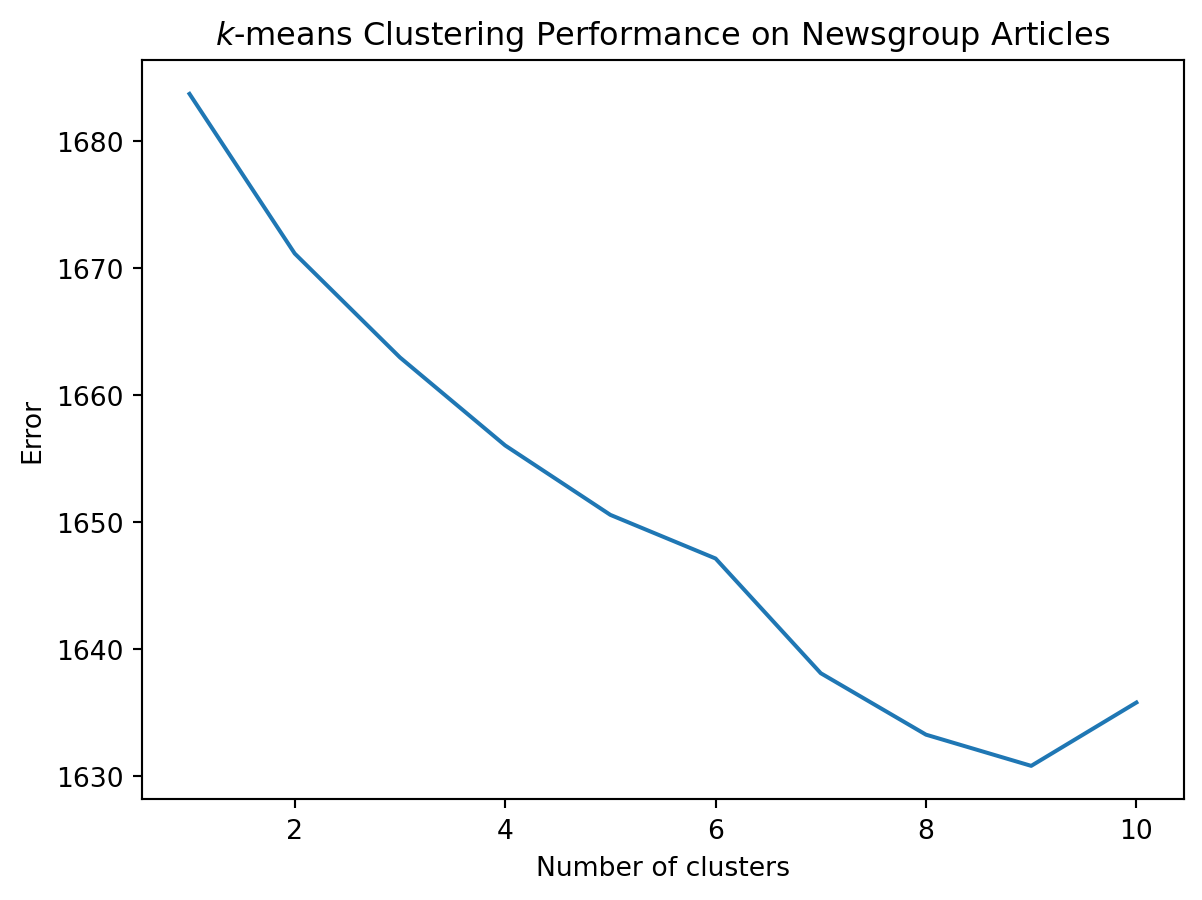
Selecting the Number of Clusters – RI
Code
ri, ari = ri_evaluate_clusters(data, 10, news_data.target)
plt.plot(range(1, len(ari)), ari[1:], 'o-')
plt.xlabel('Number of clusters')
plt.title('$k$-means Clustering Compared to Known Labels\nNewsgroup Articles')
plt.ylabel('Adjusted Rand Index')
plt.show()/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight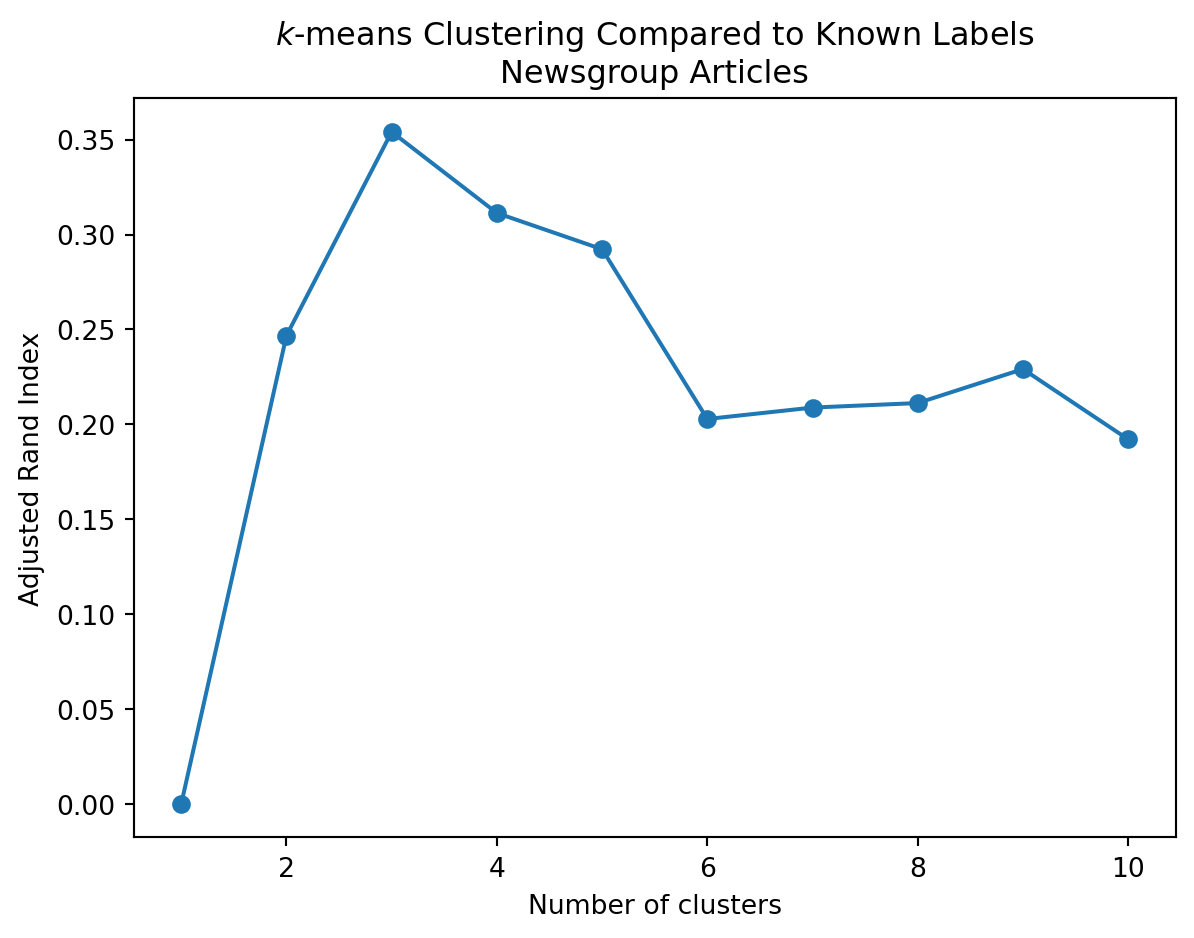
Selecting the Number of Clusters – Silhouette Score
Code
s = sc_evaluate_clusters(data, 10, 100, 3)
plt.plot(range(2, len(s)), s[2:], 'o-')
plt.xlabel('Number of Clusters')
plt.title('$k$-means clustering performance on Newsgroup Articles')
plt.ylabel('Silhouette Score')
plt.show()/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weight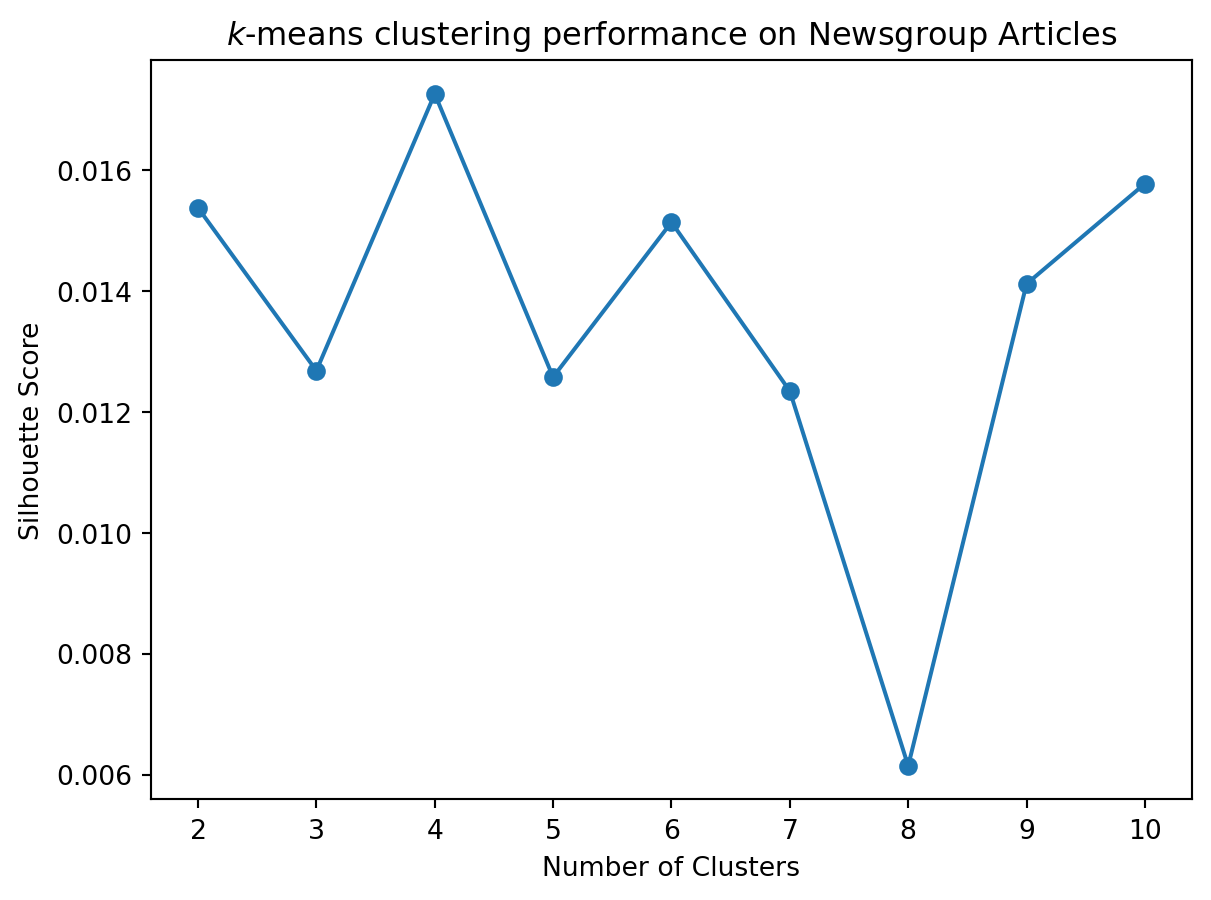
Looking into the clusters
Run \(k\)-means with 3 clusters:
Code
k = 3
kmeans = KMeans(n_clusters = k, init = 'k-means++', max_iter = 100, n_init = 25, random_state = 3)
kmeans.fit_predict(data)/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: divide by zero encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: overflow encountered in matmul
current_pot = closest_dist_sq @ sample_weight
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:237: RuntimeWarning: invalid value encountered in matmul
current_pot = closest_dist_sq @ sample_weightarray([2, 0, 0, ..., 2, 2, 2], shape=(1781,), dtype=int32)Find the top 10 terms per cluster:
Code
asc_order_centroids = kmeans.cluster_centers_.argsort()#[:, ::-1]
order_centroids = asc_order_centroids[:,::-1]
terms = vectorizer.get_feature_names_out()
for i in range(k):
print(f'Cluster {i}:')
for ind in order_centroids[i, :10]:
print(f' {terms[ind]}')
print('')Cluster 0:
windows
file
dos
files
drivers
thanks
card
driver
use
problem
Cluster 1:
year
game
team
games
runs
think
hit
good
baseball
pitching
Cluster 2:
space
like
just
think
nasa
know
don
thanks
people
does
Pairwise Distances Matrix
Let’s calculate the pairwise distances matrix.
Code
euclidean_dists = metrics.euclidean_distances(data)
labels = kmeans.labels_
idx = np.argsort(labels)
clustered_dists = euclidean_dists[idx][:,idx]
fig, ax1 = plt.subplots(1,1,figsize=(6,6))
dum = sns.heatmap(clustered_dists, xticklabels=False, yticklabels=False, linewidths=0, square=True, cbar=True, ax=ax1)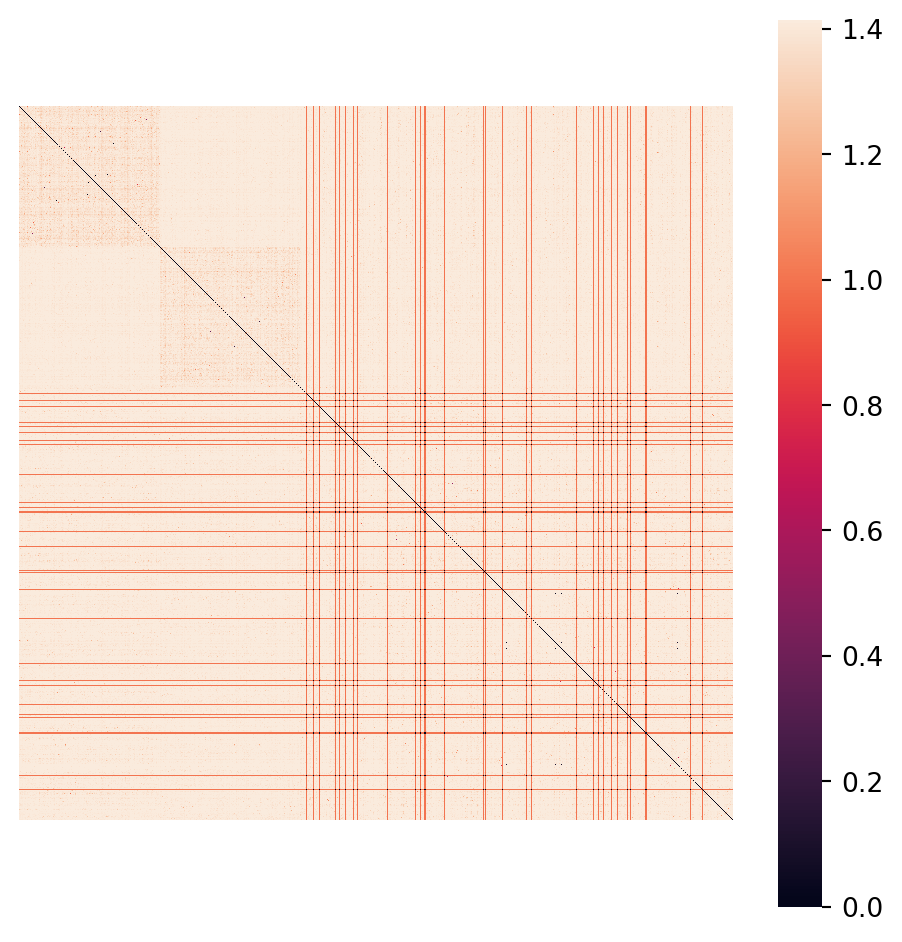
MDS Embedding
Let’s visualize with MDS.
Note that MDS is a slow algorithm and we can’t do all 1700+ data points quickly, so we will take a random sample.
Code
import random
n_items = euclidean_dists.shape[0]
random.seed(42)
subset = random.sample(range(n_items), 500)
fit = mds.fit(euclidean_dists[subset][:, subset])
pos = fit.embedding_/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
ret = a @ bWe have the labels:
Code
labelsarray([2, 0, 0, ..., 2, 2, 2], shape=(1781,), dtype=int32)MDS Embedding
Code
colorblind_palette = ['#E69F00', '#56B4E9', '#009E73', '#F0E442', '#0072B2']
cols = [colorblind_palette[l] for l in labels[subset]]
plt.scatter(pos[:, 0], pos[:, 1], s = 12, c = cols)
plt.title('MDS Embedding of Newsgroup Articles')
unique_labels = np.unique(labels[subset])
# Create legend handles and labels based on unique labels
handles = [plt.Line2D([0], [0], marker='o', color='w', markerfacecolor=colorblind_palette[l], markersize=10) for l in unique_labels]
legend_labels = [f'Cluster {l}' for l in unique_labels]
# Add the legend to the plot
plt.legend(handles, legend_labels, title='Clusters')
plt.show()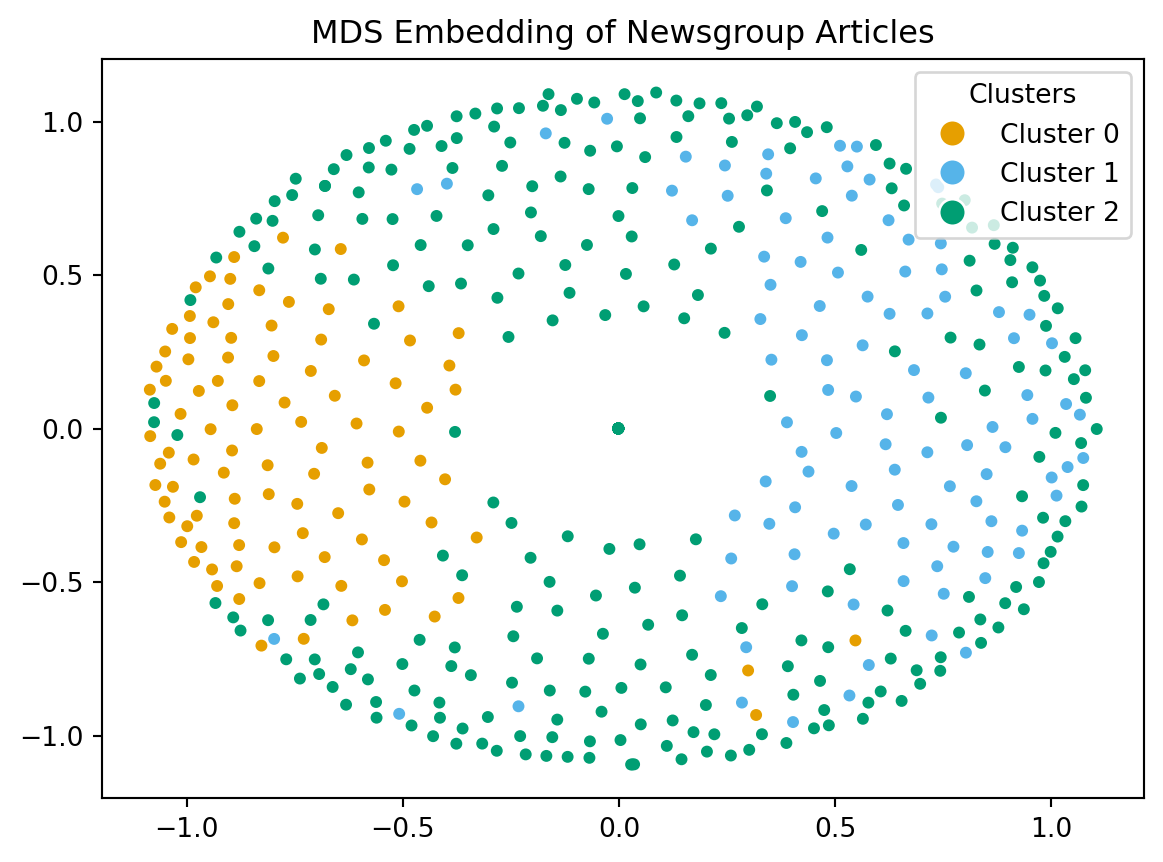
Question? Why does it produce this toroid shape?
Possible Answer: The data is high-dimensional and could be suffering from curse of dimensionality where most points are nearly the same distance from each other.
Recap and Next
We’ve covered:
- How clustering is used in practice
- Tools for evaluating the quality of a clustering
- Tools for assigning meaning or labels to a cluster
- Important visualizations
- A little bit about feature extraction for text
Next time, we’ll look at:
- Hierarchical clustering
- Gaussian mixture models