Hierarchical Clustering

Moving away from strict partitions

Code

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import pandas as pd
import sklearn.datasets as sk_data
from sklearn.cluster import KMeans

import seaborn as sns

Today we will look at a fairly different approach to clustering.
So far, we have been thinking of clustering as finding a partition of our dataset.
That is, a set of nonoverlapping clusters, in which each data item is in one cluster.
However, in many cases, the notion of a strict partition is not as useful.

Example

How Many Clusters?

How many clusters would you say there are here?

Code

X_rand, y_rand = sk_data.make_blobs(
    n_samples=[100, 100, 250, 70, 75, 80], 
    centers = [[1, 2], [1.5, 1], [3, 2], [1.75, 3.25], [2, 4], [2.25, 3.25]], 
    n_features = 2,
    center_box = (-10.0, 10.0), 
    cluster_std = [.2, .2, .3, .1, .15, .15], 
    random_state = 0
)
df_rand = pd.DataFrame(np.column_stack([X_rand[:, 0], X_rand[:, 1], y_rand]), columns = ['X', 'Y', 'label'])
df_rand = df_rand.astype({'label': 'int'})
df_rand['label3'] = [{0: 0, 1: 0, 2: 1, 3: 2, 4: 2, 5: 2}[x] for x in df_rand['label']]
df_rand['label4'] = [{0: 0, 1: 1, 2: 2, 3: 3, 4: 3, 5: 3}[x] for x in df_rand['label']]
df_rand['label5'] = [{0: 0, 1: 1, 2: 2, 3: 3, 4: 4, 5: 3}[x] for x in df_rand['label']]

# kmeans = KMeans(init = 'k-means++', n_clusters = 3, n_init = 100)
# df_rand['label'] = kmeans.fit_predict(df_rand[['X', 'Y']])

df_rand.plot('X', 'Y', kind = 'scatter',  
                   colorbar = False, figsize = (6, 6))
plt.axis('square')
plt.axis('off')
plt.show()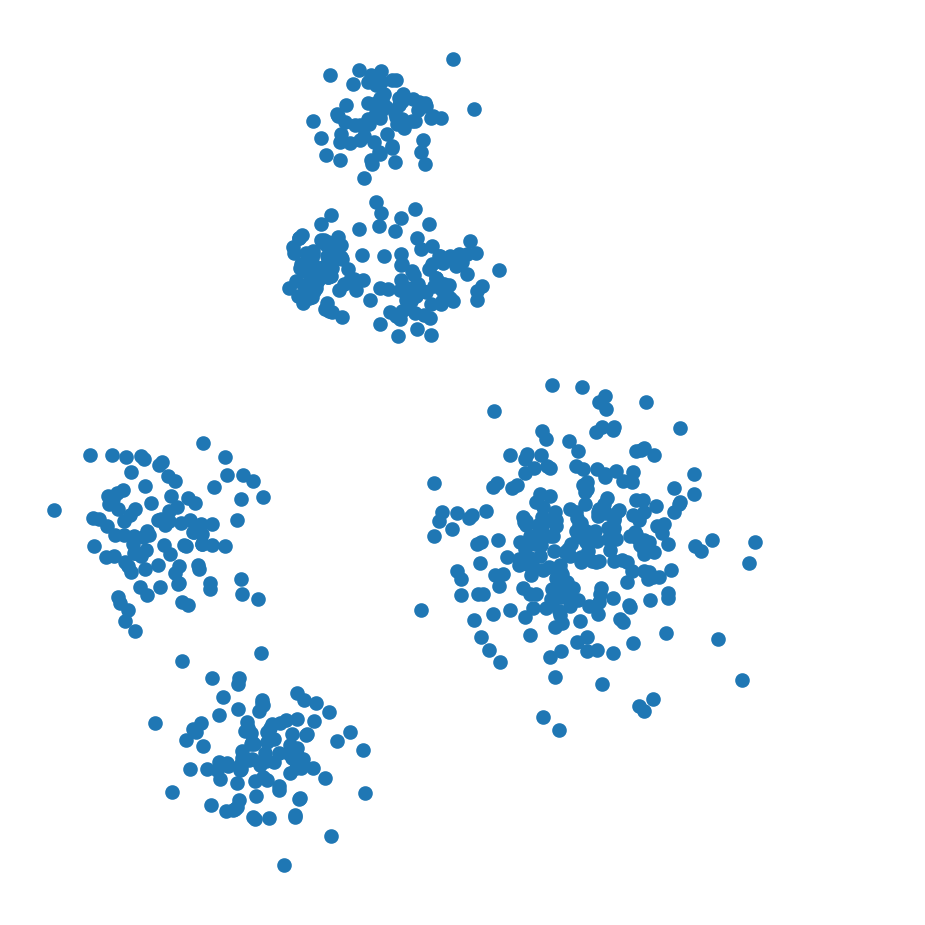

Three clusters?

Code

df_rand.plot('X', 'Y', kind = 'scatter', c = 'label3', colormap='viridis', 
                   colorbar = False, figsize = (6, 6))
plt.axis('square')
plt.axis('off')
plt.show()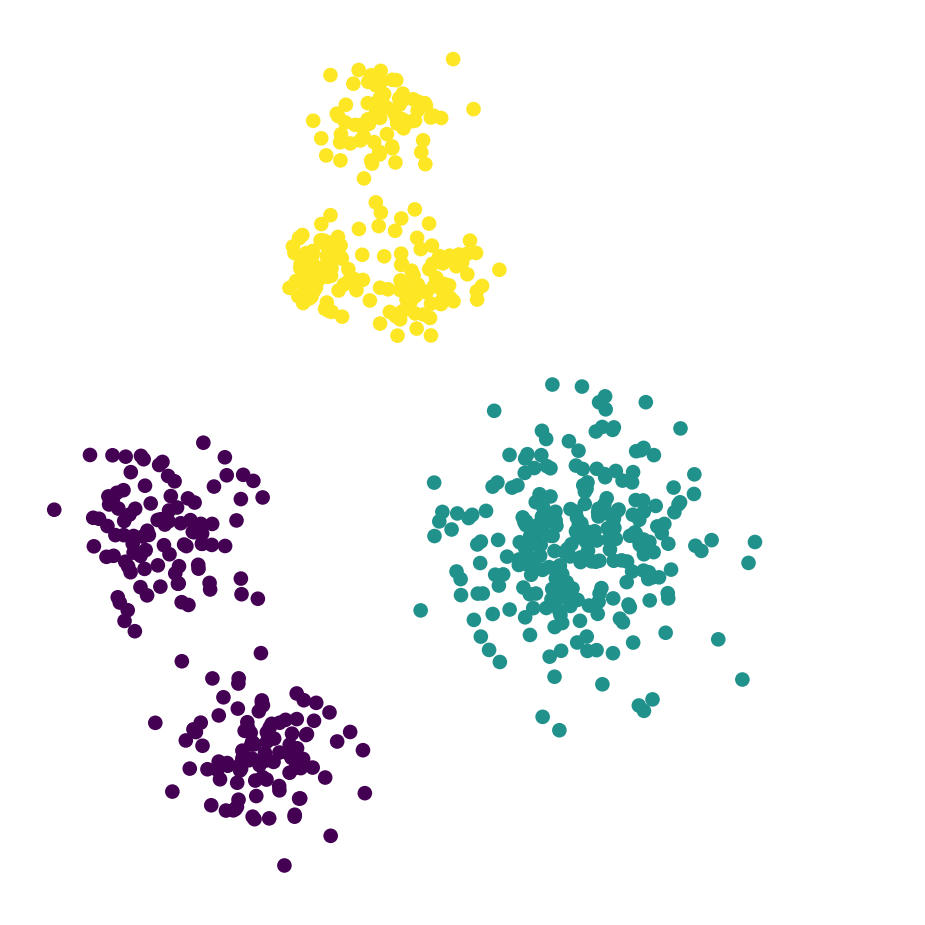

Four clusters?

Code

df_rand.plot('X', 'Y', kind = 'scatter', c = 'label4', colormap='viridis', 
                   colorbar = False, figsize = (6, 6))
plt.axis('square')
plt.axis('off')
plt.show()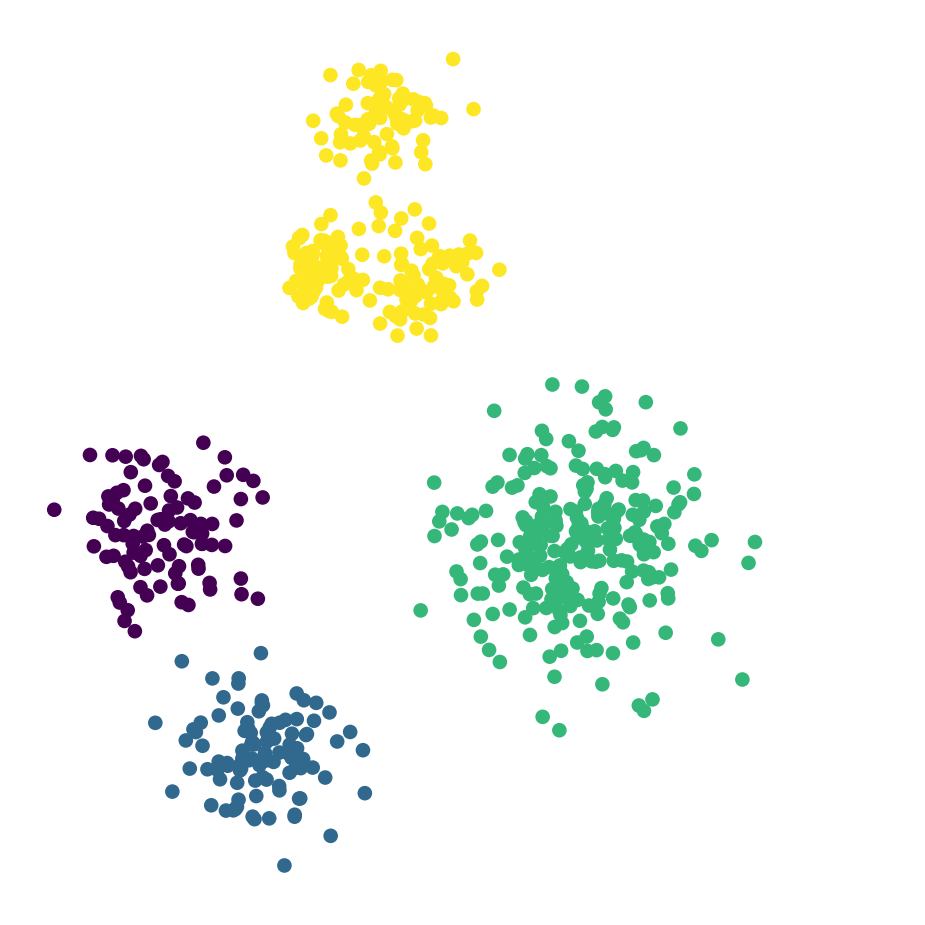

Five clusters?

Code

df_rand.plot('X', 'Y', kind = 'scatter', c = 'label5', colormap='viridis', 
                   colorbar = False, figsize = (6, 6))
plt.axis('square')
plt.axis('off')
plt.show()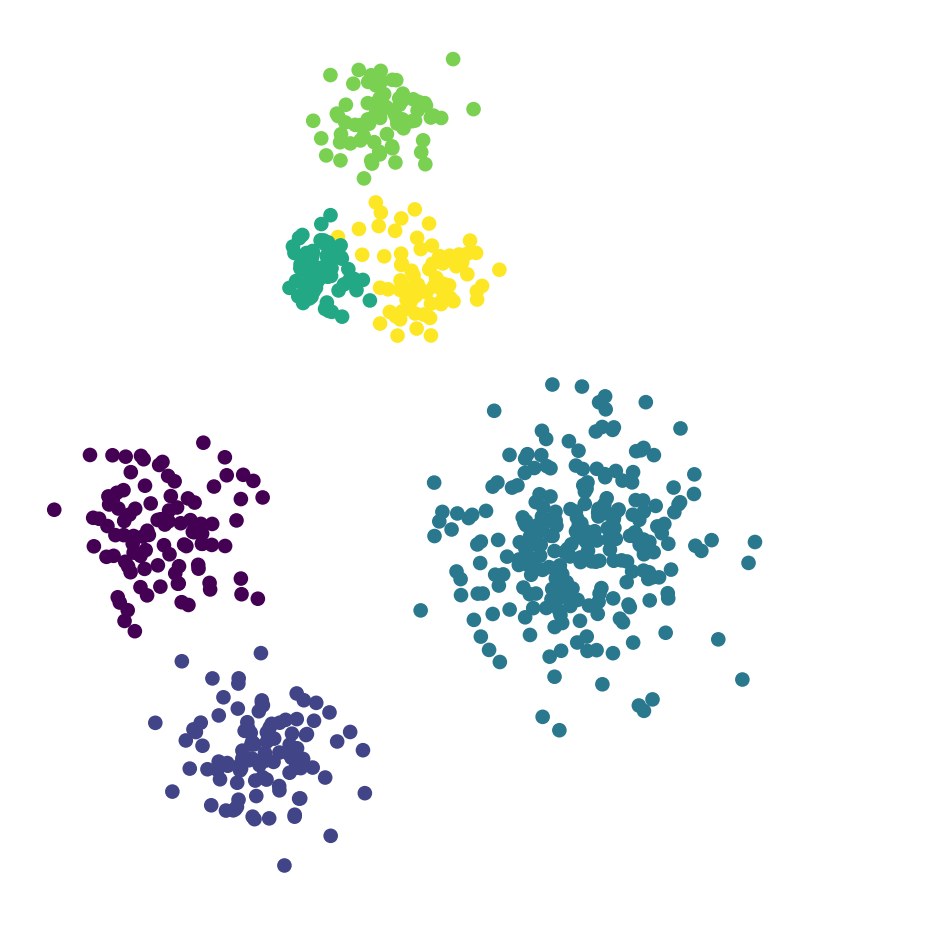

Six clusters?

Code

df_rand.plot('X', 'Y', kind = 'scatter', c = 'label', colormap='viridis', 
                   colorbar = False, figsize = (6, 6))
plt.axis('square')
plt.axis('off')
plt.show()

Code

df_rand.plot('X', 'Y', kind = 'scatter', c = 'label', colormap='viridis', 
                   colorbar = False, figsize = (4, 4))
plt.axis('square')
plt.axis('off')
plt.show()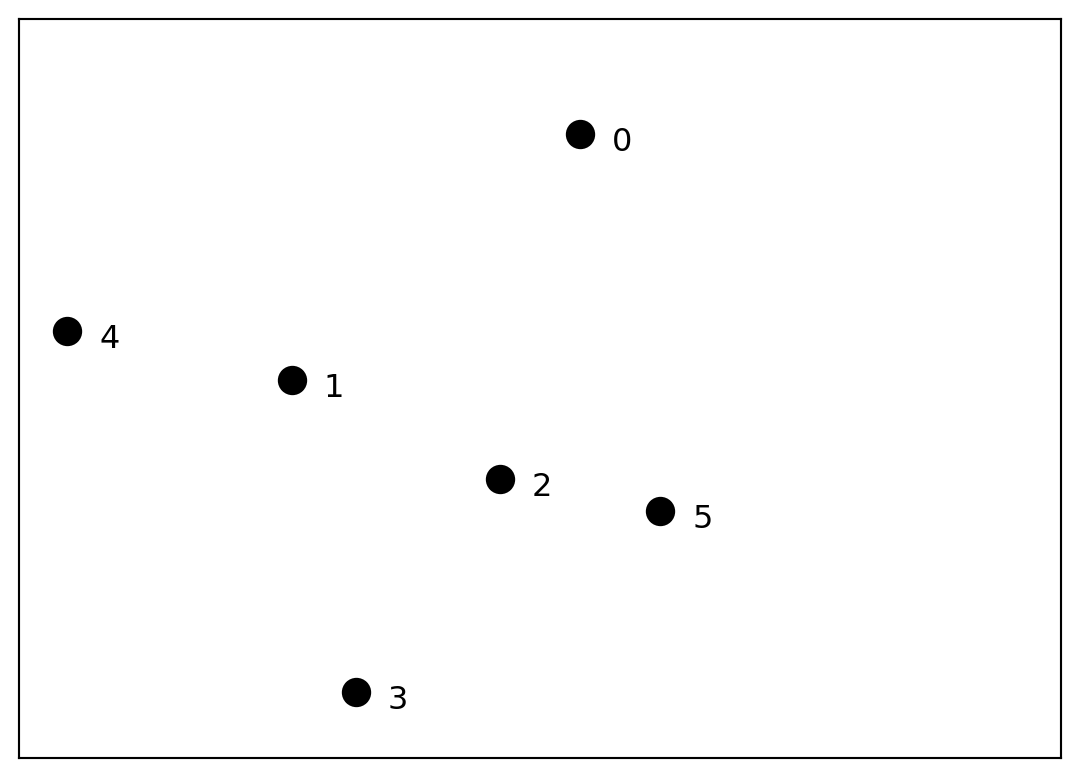

This dataset shows clustering on multiple scales.

To fully capture the structure in this dataset, two things are needed:

Capturing the differing clusters depending on the scale
Capturing the containment relations – which clusters lie within other clusters

These observations motivate the notion of hierarchical clustering.

In hierarchical clustering, we move away from the partition notion of \(k\)-means,

and instead capture a more complex arrangement that includes containment of one cluster within another.

Note: GMMs relax the partitioning notion further!

Hierarchical Clustering Example

Inspired by Hastie & Tibshirani lecture.

Code

import matplotlib.pyplot as plt
import numpy as np

# Create 5 points with labels
points = {
    'A': (1.2, 5.2),
    'B': (2.7, 4.2),
    'C': (2, 6),
    'D': (5, 3),
    'E': (4, 2)
}

# Create the scatter plot
plt.figure(figsize=(6, 6))
for label, (x, y) in points.items():
    plt.scatter(x, y, s=100, alpha=0.7)
    plt.annotate(label, (x, y), xytext=(5, 5), textcoords='offset points', 
                fontsize=12, fontweight='bold')

plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('2D Scatter Plot with 5 Labeled Points')
plt.grid(True, alpha=0.3)
plt.xlim(0, 7)
plt.ylim(0, 7)
plt.show()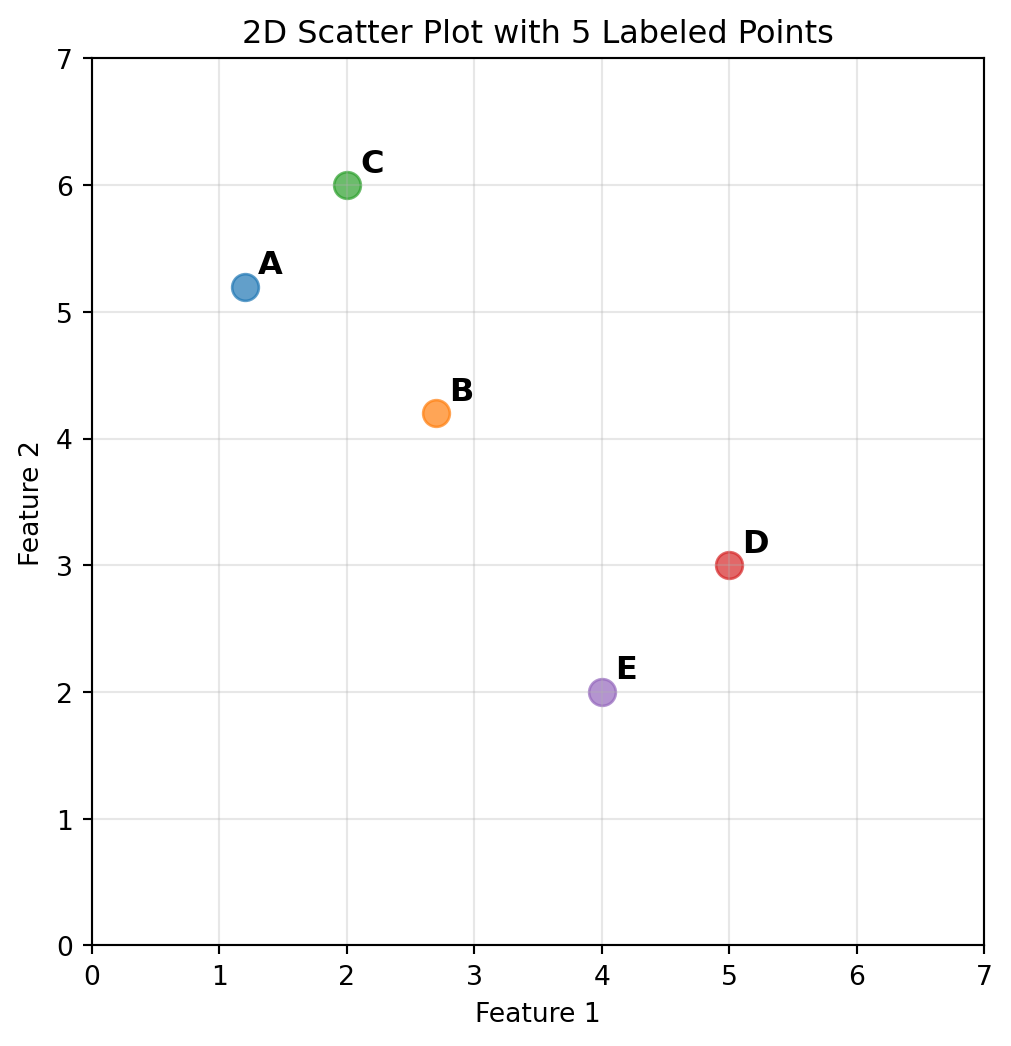

Goal: Combine closest points/clusters into a new cluster
Use distance metric to define closeness
So-called bottom-up approach or agglomerative clustering
Which 2 points are closest?

Example, cont.

Code

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Ellipse

# Create 5 points with labels (same as before)
points = {
    'A': (1.2, 5.2),
    'B': (2.7, 4.2),
    'C': (2, 6),
    'D': (5, 3),
    'E': (4, 2)
}

# Create the scatter plot
plt.figure(figsize=(6, 6))
for label, (x, y) in points.items():
    plt.scatter(x, y, s=100, alpha=0.7)
    plt.annotate(label, (x, y), xytext=(5, 5), textcoords='offset points', 
                fontsize=12, fontweight='bold')

# Draw an ellipse around points A and C where A and C are the foci
A_x, A_y = points['A']
C_x, C_y = points['C']

# Calculate the distance between foci (A and C)
focal_distance = np.sqrt((C_x - A_x)**2 + (C_y - A_y)**2)

# Calculate center of ellipse (midpoint between foci)
center_x = (A_x + C_x) / 2
center_y = (A_y + C_y) / 2

# Calculate the angle of the major axis
angle = np.degrees(np.arctan2(C_y - A_y, C_x - A_x))

# Set semi-major axis (a) and semi-minor axis (b)
# For an ellipse: c = sqrt(a^2 - b^2) where c is half the focal distance
# We'll set a = focal_distance/2 + padding, then calculate b
a = focal_distance/2 + 0.4  # semi-major axis with padding
c = focal_distance/2  # half the focal distance
b = np.sqrt(a**2 - c**2)  # semi-minor axis

# Create and add the ellipse
ellipse = Ellipse((center_x, center_y), 2*a, 2*b, angle=angle,
                  facecolor='none', edgecolor='red', linewidth=2, linestyle='--')
plt.gca().add_patch(ellipse)

plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('2D Scatter Plot - First Cluster (A & C)')
plt.grid(True, alpha=0.3)
plt.xlim(0, 7)
plt.ylim(0, 7)
plt.show()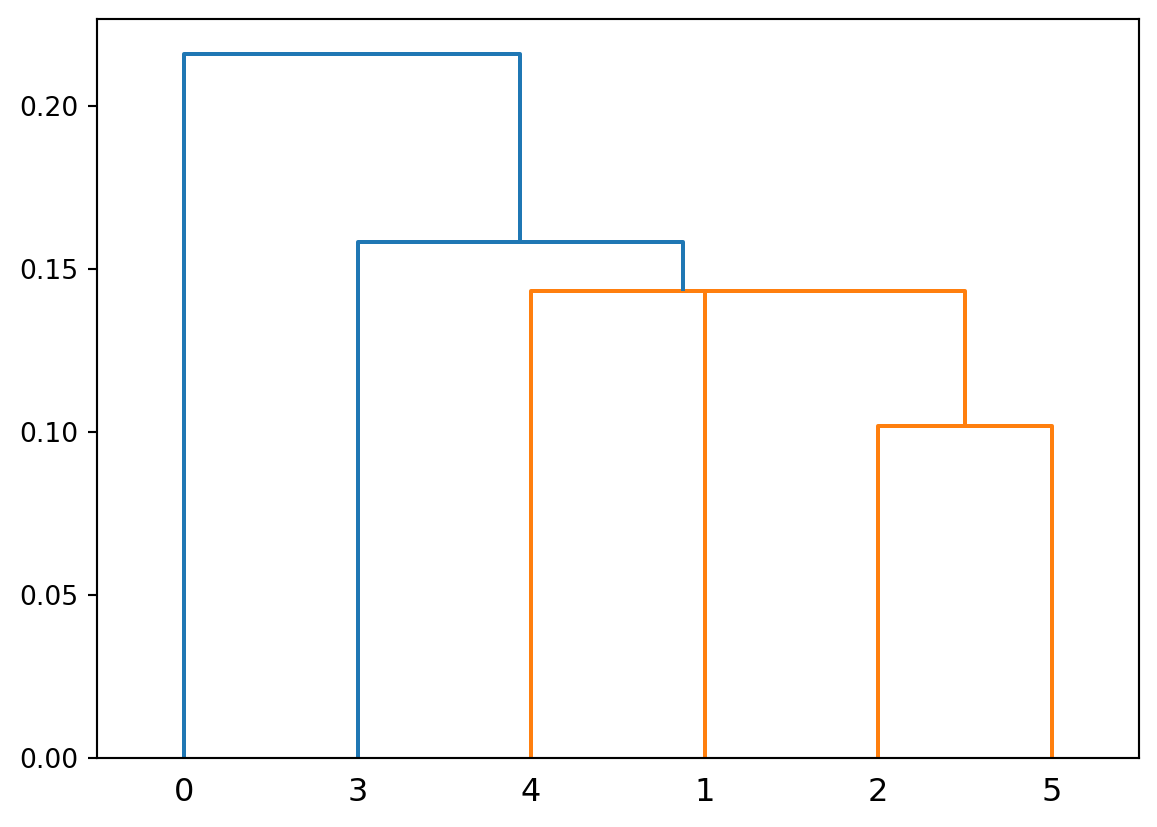

Now we want to combine either the next closest pair of points or the point closest to a cluster
How do we measure closeness of points to clusters?
Or clusters to clusters?

Example, cont. (Part 2)

Code

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Ellipse

# Create 5 points with labels (same as before)
points = {
    'A': (1.2, 5.2),
    'B': (2.7, 4.2),
    'C': (2, 6),
    'D': (5, 3),
    'E': (4, 2)
}

# Create the scatter plot
plt.figure(figsize=(6, 6))
for label, (x, y) in points.items():
    plt.scatter(x, y, s=100, alpha=0.7)
    plt.annotate(label, (x, y), xytext=(5, 5), textcoords='offset points', 
                fontsize=12, fontweight='bold')

# Draw an ellipse around points A and C where A and C are the foci
A_x, A_y = points['A']
C_x, C_y = points['C']

# Calculate the distance between foci (A and C)
focal_distance = np.sqrt((C_x - A_x)**2 + (C_y - A_y)**2)

# Calculate center of ellipse (midpoint between foci)
center_x = (A_x + C_x) / 2
center_y = (A_y + C_y) / 2

# Calculate the angle of the major axis
angle = np.degrees(np.arctan2(C_y - A_y, C_x - A_x))

# Set semi-major axis (a) and semi-minor axis (b)
# For an ellipse: c = sqrt(a^2 - b^2) where c is half the focal distance
# We'll set a = focal_distance/2 + padding, then calculate b
a = focal_distance/2 + 0.4  # semi-major axis with padding
c = focal_distance/2  # half the focal distance
b = np.sqrt(a**2 - c**2)  # semi-minor axis

# Create and add the ellipse for A and C
ellipse1 = Ellipse((center_x, center_y), 2*a, 2*b, angle=angle,
                   facecolor='none', edgecolor='red', linewidth=2, linestyle='--')
plt.gca().add_patch(ellipse1)

# Draw an ellipse around points E and D where E and D are the foci
E_x, E_y = points['E']
D_x, D_y = points['D']

# Calculate the distance between foci (E and D)
focal_distance_ED = np.sqrt((D_x - E_x)**2 + (D_y - E_y)**2)

# Calculate center of ellipse (midpoint between foci)
center_x_ED = (E_x + D_x) / 2
center_y_ED = (E_y + D_y) / 2

# Calculate the angle of the major axis
angle_ED = np.degrees(np.arctan2(D_y - E_y, D_x - E_x))

# Set semi-major axis (a) and semi-minor axis (b)
a_ED = focal_distance_ED/2 + 0.4  # semi-major axis with padding
c_ED = focal_distance_ED/2  # half the focal distance
b_ED = np.sqrt(a_ED**2 - c_ED**2)  # semi-minor axis

# Create and add the ellipse for E and D
ellipse2 = Ellipse((center_x_ED, center_y_ED), 2*a_ED, 2*b_ED, angle=angle_ED,
                   facecolor='none', edgecolor='blue', linewidth=2, linestyle='--')
plt.gca().add_patch(ellipse2)

plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('2D Scatter Plot - Two Clusters (A&C, E&D)')
plt.grid(True, alpha=0.3)
plt.xlim(0, 7)
plt.ylim(0, 7)
plt.show()

Assume D and E are the next closest pair of points
Now which cluster is B closest to?

Example, cont. (Part 3)

Code

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Ellipse

# Create 5 points with labels (same as before)
points = {
    'A': (1.2, 5.2),
    'B': (2.7, 4.2),
    'C': (2, 6),
    'D': (5, 3),
    'E': (4, 2)
}

# Create the scatter plot
plt.figure(figsize=(6, 6))
for label, (x, y) in points.items():
    plt.scatter(x, y, s=100, alpha=0.7)
    plt.annotate(label, (x, y), xytext=(5, 5), textcoords='offset points', 
                fontsize=12, fontweight='bold')

# Draw an ellipse around points A and C where A and C are the foci
A_x, A_y = points['A']
C_x, C_y = points['C']

# Calculate the distance between foci (A and C)
focal_distance = np.sqrt((C_x - A_x)**2 + (C_y - A_y)**2)

# Calculate center of ellipse (midpoint between foci)
center_x = (A_x + C_x) / 2
center_y = (A_y + C_y) / 2

# Calculate the angle of the major axis
angle = np.degrees(np.arctan2(C_y - A_y, C_x - A_x))

# Set semi-major axis (a) and semi-minor axis (b)
# For an ellipse: c = sqrt(a^2 - b^2) where c is half the focal distance
# We'll set a = focal_distance/2 + padding, then calculate b
a = focal_distance/2 + 0.4  # semi-major axis with padding
c = focal_distance/2  # half the focal distance
b = np.sqrt(a**2 - c**2)  # semi-minor axis

# Create and add the ellipse for A and C
ellipse1 = Ellipse((center_x, center_y), 2*a, 2*b, angle=angle,
                   facecolor='none', edgecolor='red', linewidth=2, linestyle='--')
plt.gca().add_patch(ellipse1)

# Draw an ellipse around points E and D where E and D are the foci
E_x, E_y = points['E']
D_x, D_y = points['D']

# Calculate the distance between foci (E and D)
focal_distance_ED = np.sqrt((D_x - E_x)**2 + (D_y - E_y)**2)

# Calculate center of ellipse (midpoint between foci)
center_x_ED = (E_x + D_x) / 2
center_y_ED = (E_y + D_y) / 2

# Calculate the angle of the major axis
angle_ED = np.degrees(np.arctan2(D_y - E_y, D_x - E_x))

# Set semi-major axis (a) and semi-minor axis (b)
a_ED = focal_distance_ED/2 + 0.4  # semi-major axis with padding
c_ED = focal_distance_ED/2  # half the focal distance
b_ED = np.sqrt(a_ED**2 - c_ED**2)  # semi-minor axis

# Create and add the ellipse for E and D
ellipse2 = Ellipse((center_x_ED, center_y_ED), 2*a_ED, 2*b_ED, angle=angle_ED,
                   facecolor='none', edgecolor='blue', linewidth=2, linestyle='--')
plt.gca().add_patch(ellipse2)

# Draw a circle around points A, B, and C
A_x, A_y = points['A']
B_x, B_y = points['B']
C_x, C_y = points['C']

# Calculate the center of the circle (centroid of the three points)
center_x_ABC = (A_x + B_x + C_x) / 3
center_y_ABC = (A_y + B_y + C_y) / 3

# Calculate the radius as the maximum distance from center to any of the three points
dist_A = np.sqrt((A_x - center_x_ABC)**2 + (A_y - center_y_ABC)**2)
dist_B = np.sqrt((B_x - center_x_ABC)**2 + (B_y - center_y_ABC)**2)
dist_C = np.sqrt((C_x - center_x_ABC)**2 + (C_y - center_y_ABC)**2)
radius_ABC = max(dist_A, dist_B, dist_C) + 0.3  # Add some padding

# Create and add the circle
circle = plt.Circle((center_x_ABC, center_y_ABC), radius_ABC,
                   facecolor='none', edgecolor='green', linewidth=2, linestyle='--')
plt.gca().add_patch(circle)

plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('2D Scatter Plot - Three Clusters')
plt.grid(True, alpha=0.3)
plt.xlim(0, 7)
plt.ylim(0, 7)
plt.show()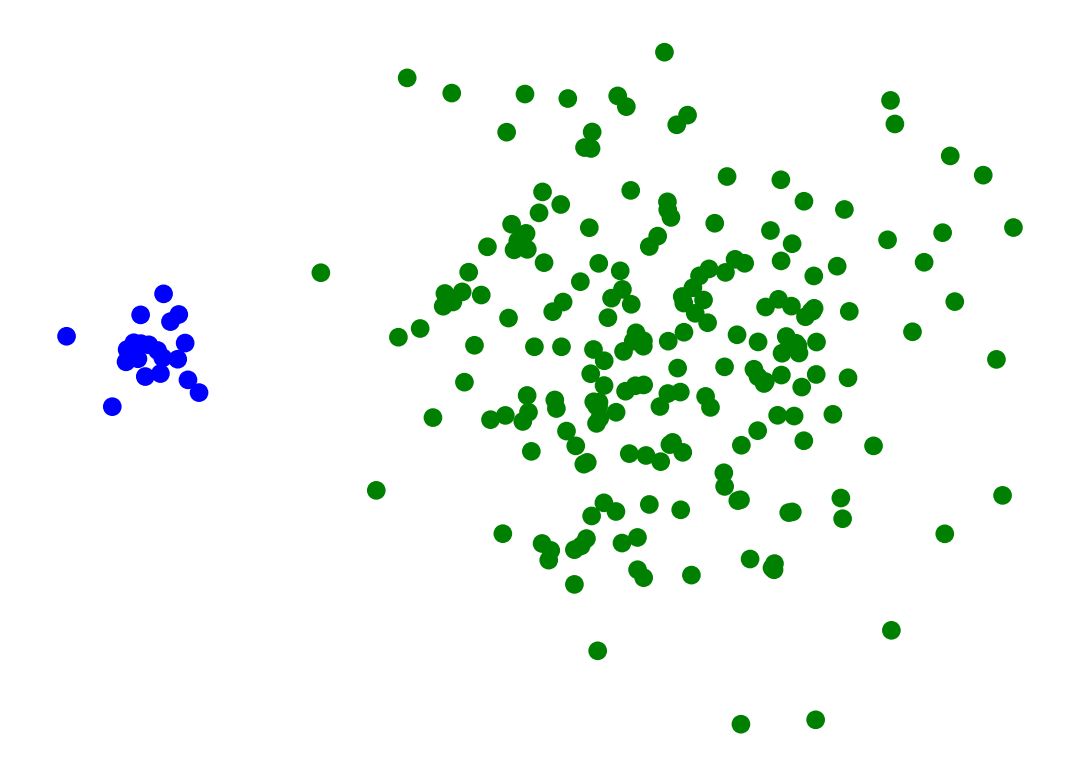

We’ll talk about measuring distances between clusters shortly
But let’s just say that B is closest to the cluster A, C, E and forms a new cluster
and then finally…

Example, cont. (Part 4)

Code

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Ellipse

# Create 5 points with labels (same as before)
points = {
    'A': (1.2, 5.2),
    'B': (2.7, 4.2),
    'C': (2, 6),
    'D': (5, 3),
    'E': (4, 2)
}

# Create the scatter plot
plt.figure(figsize=(6, 6))
for label, (x, y) in points.items():
    plt.scatter(x, y, s=100, alpha=0.7)
    plt.annotate(label, (x, y), xytext=(5, 5), textcoords='offset points', 
                fontsize=12, fontweight='bold')

# Draw an ellipse around points A and C where A and C are the foci
A_x, A_y = points['A']
C_x, C_y = points['C']

# Calculate the distance between foci (A and C)
focal_distance = np.sqrt((C_x - A_x)**2 + (C_y - A_y)**2)

# Calculate center of ellipse (midpoint between foci)
center_x = (A_x + C_x) / 2
center_y = (A_y + C_y) / 2

# Calculate the angle of the major axis
angle = np.degrees(np.arctan2(C_y - A_y, C_x - A_x))

# Set semi-major axis (a) and semi-minor axis (b)
# For an ellipse: c = sqrt(a^2 - b^2) where c is half the focal distance
# We'll set a = focal_distance/2 + padding, then calculate b
a = focal_distance/2 + 0.4  # semi-major axis with padding
c = focal_distance/2  # half the focal distance
b = np.sqrt(a**2 - c**2)  # semi-minor axis

# Create and add the ellipse for A and C
ellipse1 = Ellipse((center_x, center_y), 2*a, 2*b, angle=angle,
                   facecolor='none', edgecolor='red', linewidth=2, linestyle='--')
plt.gca().add_patch(ellipse1)

# Draw an ellipse around points E and D where E and D are the foci
E_x, E_y = points['E']
D_x, D_y = points['D']

# Calculate the distance between foci (E and D)
focal_distance_ED = np.sqrt((D_x - E_x)**2 + (D_y - E_y)**2)

# Calculate center of ellipse (midpoint between foci)
center_x_ED = (E_x + D_x) / 2
center_y_ED = (E_y + D_y) / 2

# Calculate the angle of the major axis
angle_ED = np.degrees(np.arctan2(D_y - E_y, D_x - E_x))

# Set semi-major axis (a) and semi-minor axis (b)
a_ED = focal_distance_ED/2 + 0.4  # semi-major axis with padding
c_ED = focal_distance_ED/2  # half the focal distance
b_ED = np.sqrt(a_ED**2 - c_ED**2)  # semi-minor axis

# Create and add the ellipse for E and D
ellipse2 = Ellipse((center_x_ED, center_y_ED), 2*a_ED, 2*b_ED, angle=angle_ED,
                   facecolor='none', edgecolor='blue', linewidth=2, linestyle='--')
plt.gca().add_patch(ellipse2)

# Draw a circle around points A, B, and C
A_x, A_y = points['A']
B_x, B_y = points['B']
C_x, C_y = points['C']

# Calculate the center of the circle (centroid of the three points)
center_x_ABC = (A_x + B_x + C_x) / 3
center_y_ABC = (A_y + B_y + C_y) / 3

# Calculate the radius as the maximum distance from center to any of the three points
dist_A = np.sqrt((A_x - center_x_ABC)**2 + (A_y - center_y_ABC)**2)
dist_B = np.sqrt((B_x - center_x_ABC)**2 + (B_y - center_y_ABC)**2)
dist_C = np.sqrt((C_x - center_x_ABC)**2 + (C_y - center_y_ABC)**2)
radius_ABC = max(dist_A, dist_B, dist_C) + 0.3  # Add some padding

# Create and add the circle
circle = plt.Circle((center_x_ABC, center_y_ABC), radius_ABC,
                   facecolor='none', edgecolor='green', linewidth=2, linestyle='--')
plt.gca().add_patch(circle)

# Draw an ellipse around all 5 points
all_x = [points[label][0] for label in points.keys()]
all_y = [points[label][1] for label in points.keys()]

# Calculate center of ellipse (centroid of all points)
center_x_all = np.mean(all_x)
center_y_all = np.mean(all_y)




width_all, height_all = 3.2, 7
angle_all = 40

print(width_all, height_all, angle_all, center_x_all, center_y_all)

# Create and add the ellipse around all points
ellipse_all = Ellipse((center_x_all, center_y_all), width_all, height_all, angle=angle_all,
                     facecolor='none', edgecolor='purple', linewidth=3, linestyle='-')
plt.gca().add_patch(ellipse_all)

plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('2D Scatter Plot - Final Cluster (All Points)')
plt.grid(True, alpha=0.3)
plt.xlim(0, 7)
plt.ylim(0, 7)
plt.show()

3.2 7 40 2.98 4.08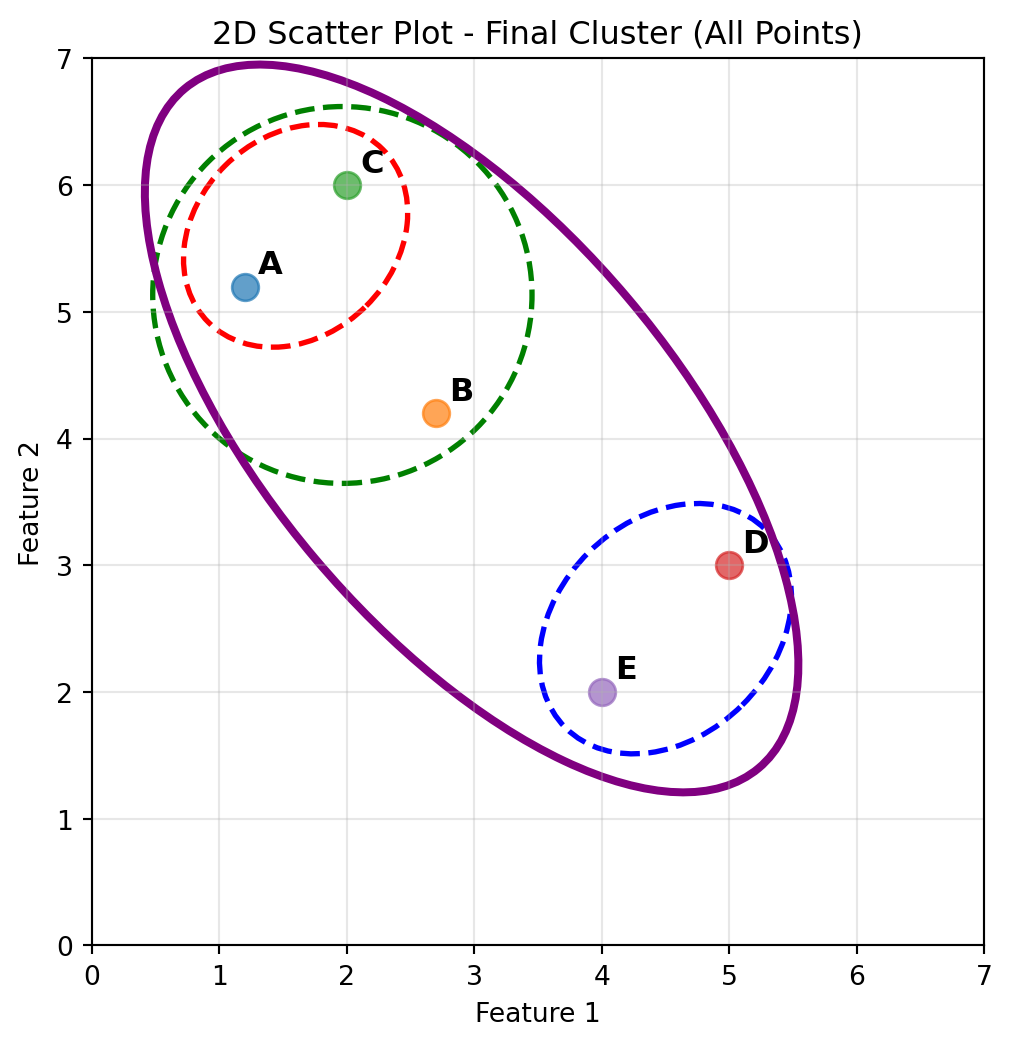

We combine all points into a single cluster

Example: Dendrogram

Code

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Ellipse
from scipy.cluster.hierarchy import dendrogram, linkage
from scipy.spatial.distance import pdist

# Create 5 points with labels (same as before)
points = {
    'A': (1.2, 5.2),
    'B': (2.7, 4.2),
    'C': (2, 6),
    'D': (5, 3),
    'E': (4, 2)
}

# Create figure with two subplots
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 6))

# First subplot: Scatter plot with clusters
for label, (x, y) in points.items():
    ax1.scatter(x, y, s=100, alpha=0.7)
    ax1.annotate(label, (x, y), xytext=(5, 5), textcoords='offset points', 
                fontsize=12, fontweight='bold')

# Draw an ellipse around points A and C where A and C are the foci
A_x, A_y = points['A']
C_x, C_y = points['C']

# Calculate the distance between foci (A and C)
focal_distance = np.sqrt((C_x - A_x)**2 + (C_y - A_y)**2)

# Calculate center of ellipse (midpoint between foci)
center_x = (A_x + C_x) / 2
center_y = (A_y + C_y) / 2

# Calculate the angle of the major axis
angle = np.degrees(np.arctan2(C_y - A_y, C_x - A_x))

# Set semi-major axis (a) and semi-minor axis (b)
a = focal_distance/2 + 0.4  # semi-major axis with padding
c = focal_distance/2  # half the focal distance
b = np.sqrt(a**2 - c**2)  # semi-minor axis

# Create and add the ellipse for A and C
ellipse1 = Ellipse((center_x, center_y), 2*a, 2*b, angle=angle,
                   facecolor='none', edgecolor='red', linewidth=2, linestyle='--')
ax1.add_patch(ellipse1)

# Draw an ellipse around points E and D where E and D are the foci
E_x, E_y = points['E']
D_x, D_y = points['D']

# Calculate the distance between foci (E and D)
focal_distance_ED = np.sqrt((D_x - E_x)**2 + (D_y - E_y)**2)

# Calculate center of ellipse (midpoint between foci)
center_x_ED = (E_x + D_x) / 2
center_y_ED = (E_y + D_y) / 2

# Calculate the angle of the major axis
angle_ED = np.degrees(np.arctan2(D_y - E_y, D_x - E_x))

# Set semi-major axis (a) and semi-minor axis (b)
a_ED = focal_distance_ED/2 + 0.4  # semi-major axis with padding
c_ED = focal_distance_ED/2  # half the focal distance
b_ED = np.sqrt(a_ED**2 - c_ED**2)  # semi-minor axis

# Create and add the ellipse for E and D
ellipse2 = Ellipse((center_x_ED, center_y_ED), 2*a_ED, 2*b_ED, angle=angle_ED,
                   facecolor='none', edgecolor='blue', linewidth=2, linestyle='--')
ax1.add_patch(ellipse2)

# Draw a circle around points A, B, and C
A_x, A_y = points['A']
B_x, B_y = points['B']
C_x, C_y = points['C']

# Calculate the center of the circle (centroid of the three points)
center_x_ABC = (A_x + B_x + C_x) / 3
center_y_ABC = (A_y + B_y + C_y) / 3

# Calculate the radius as the maximum distance from center to any of the three points
dist_A = np.sqrt((A_x - center_x_ABC)**2 + (A_y - center_y_ABC)**2)
dist_B = np.sqrt((B_x - center_x_ABC)**2 + (B_y - center_y_ABC)**2)
dist_C = np.sqrt((C_x - center_x_ABC)**2 + (C_y - center_y_ABC)**2)
radius_ABC = max(dist_A, dist_B, dist_C) + 0.3  # Add some padding

# Create and add the circle
circle = plt.Circle((center_x_ABC, center_y_ABC), radius_ABC,
                   facecolor='none', edgecolor='green', linewidth=2, linestyle='--')
ax1.add_patch(circle)

# Draw an ellipse around all 5 points
all_x = [points[label][0] for label in points.keys()]
all_y = [points[label][1] for label in points.keys()]

# Calculate center of ellipse (centroid of all points)
center_x_all = np.mean(all_x)
center_y_all = np.mean(all_y)

width_all, height_all = 3.2, 7
angle_all = 40

# Create and add the ellipse around all points
ellipse_all = Ellipse((center_x_all, center_y_all), width_all, height_all, angle=angle_all,
                     facecolor='none', edgecolor='purple', linewidth=3, linestyle='-')
ax1.add_patch(ellipse_all)

ax1.set_xlabel('Feature 1')
ax1.set_ylabel('Feature 2')
ax1.set_title('Clusters at Different Levels')
ax1.grid(True, alpha=0.3)
ax1.set_xlim(0, 7)
ax1.set_ylim(0, 7)

# Second subplot: Dendrogram
# Prepare data for hierarchical clustering
points_array = np.array(list(points.values()))
point_labels = list(points.keys())

# Calculate linkage matrix
linkage_matrix = linkage(points_array, method='ward')

# Create dendrogram
dendrogram(linkage_matrix, labels=point_labels, ax=ax2, 
          leaf_rotation=0, leaf_font_size=12)
ax2.set_title('Hierarchical Clustering Dendrogram')
ax2.set_xlabel('Points')
ax2.set_ylabel('Distance')

plt.tight_layout()
plt.show()

Example: Dendrogram Explained

Code

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Ellipse
from scipy.cluster.hierarchy import dendrogram, linkage
from scipy.spatial.distance import pdist

# Create 5 points with labels (same as before)
points = {
    'A': (1.2, 5.2),
    'B': (2.7, 4.2),
    'C': (2, 6),
    'D': (5, 3),
    'E': (4, 2)
}

# Create figure with two subplots
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(6, 3))

# First subplot: Scatter plot with clusters
for label, (x, y) in points.items():
    ax1.scatter(x, y, s=100, alpha=0.7)
    ax1.annotate(label, (x, y), xytext=(5, 5), textcoords='offset points', 
                fontsize=12, fontweight='bold')

# Draw an ellipse around points A and C where A and C are the foci
A_x, A_y = points['A']
C_x, C_y = points['C']

# Calculate the distance between foci (A and C)
focal_distance = np.sqrt((C_x - A_x)**2 + (C_y - A_y)**2)

# Calculate center of ellipse (midpoint between foci)
center_x = (A_x + C_x) / 2
center_y = (A_y + C_y) / 2

# Calculate the angle of the major axis
angle = np.degrees(np.arctan2(C_y - A_y, C_x - A_x))

# Set semi-major axis (a) and semi-minor axis (b)
a = focal_distance/2 + 0.4  # semi-major axis with padding
c = focal_distance/2  # half the focal distance
b = np.sqrt(a**2 - c**2)  # semi-minor axis

# Create and add the ellipse for A and C
ellipse1 = Ellipse((center_x, center_y), 2*a, 2*b, angle=angle,
                   facecolor='none', edgecolor='red', linewidth=2, linestyle='--')
ax1.add_patch(ellipse1)

# Draw an ellipse around points E and D where E and D are the foci
E_x, E_y = points['E']
D_x, D_y = points['D']

# Calculate the distance between foci (E and D)
focal_distance_ED = np.sqrt((D_x - E_x)**2 + (D_y - E_y)**2)

# Calculate center of ellipse (midpoint between foci)
center_x_ED = (E_x + D_x) / 2
center_y_ED = (E_y + D_y) / 2

# Calculate the angle of the major axis
angle_ED = np.degrees(np.arctan2(D_y - E_y, D_x - E_x))

# Set semi-major axis (a) and semi-minor axis (b)
a_ED = focal_distance_ED/2 + 0.4  # semi-major axis with padding
c_ED = focal_distance_ED/2  # half the focal distance
b_ED = np.sqrt(a_ED**2 - c_ED**2)  # semi-minor axis

# Create and add the ellipse for E and D
ellipse2 = Ellipse((center_x_ED, center_y_ED), 2*a_ED, 2*b_ED, angle=angle_ED,
                   facecolor='none', edgecolor='blue', linewidth=2, linestyle='--')
ax1.add_patch(ellipse2)

# Draw a circle around points A, B, and C
A_x, A_y = points['A']
B_x, B_y = points['B']
C_x, C_y = points['C']

# Calculate the center of the circle (centroid of the three points)
center_x_ABC = (A_x + B_x + C_x) / 3
center_y_ABC = (A_y + B_y + C_y) / 3

# Calculate the radius as the maximum distance from center to any of the three points
dist_A = np.sqrt((A_x - center_x_ABC)**2 + (A_y - center_y_ABC)**2)
dist_B = np.sqrt((B_x - center_x_ABC)**2 + (B_y - center_y_ABC)**2)
dist_C = np.sqrt((C_x - center_x_ABC)**2 + (C_y - center_y_ABC)**2)
radius_ABC = max(dist_A, dist_B, dist_C) + 0.3  # Add some padding

# Create and add the circle
circle = plt.Circle((center_x_ABC, center_y_ABC), radius_ABC,
                   facecolor='none', edgecolor='green', linewidth=2, linestyle='--')
ax1.add_patch(circle)

# Draw an ellipse around all 5 points
all_x = [points[label][0] for label in points.keys()]
all_y = [points[label][1] for label in points.keys()]

# Calculate center of ellipse (centroid of all points)
center_x_all = np.mean(all_x)
center_y_all = np.mean(all_y)

width_all, height_all = 3.2, 7
angle_all = 40

# Create and add the ellipse around all points
ellipse_all = Ellipse((center_x_all, center_y_all), width_all, height_all, angle=angle_all,
                     facecolor='none', edgecolor='purple', linewidth=3, linestyle='-')
ax1.add_patch(ellipse_all)

ax1.set_xlabel('Feature 1')
ax1.set_ylabel('Feature 2')
ax1.set_title('Clusters at Different Levels')
ax1.grid(True, alpha=0.3)
ax1.set_xlim(0, 7)
ax1.set_ylim(0, 7)

# Second subplot: Dendrogram
# Prepare data for hierarchical clustering
points_array = np.array(list(points.values()))
point_labels = list(points.keys())

# Calculate linkage matrix
linkage_matrix = linkage(points_array, method='ward')

# Create dendrogram
dendrogram(linkage_matrix, labels=point_labels, ax=ax2, 
          leaf_rotation=0, leaf_font_size=12)
ax2.set_title('Hierarchical Clustering Dendrogram')
ax2.set_xlabel('Points')
ax2.set_ylabel('Distance')

plt.tight_layout()
plt.show()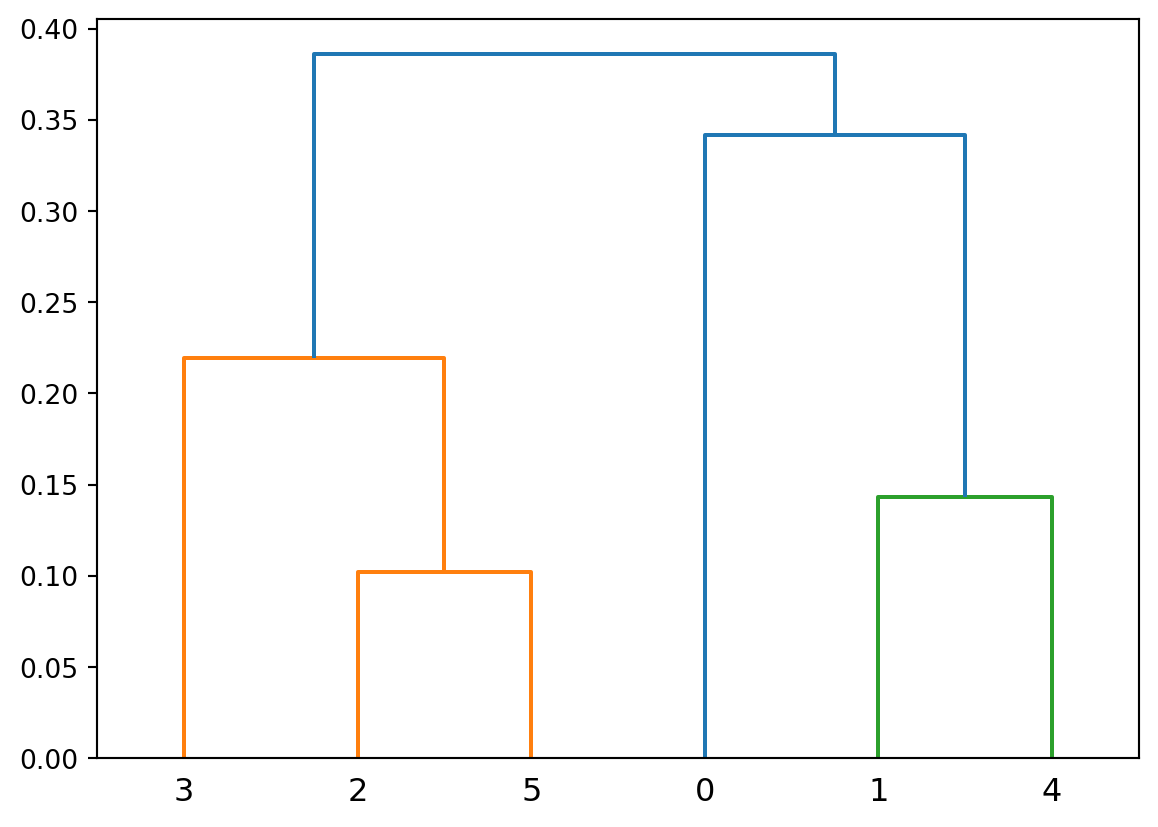

In the dendrogram, the vertical axis is the distance between the clusters
The horizontal axis is the points
The clusters are merged from the bottom up

Example: Dendrogram cont.

Code

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Ellipse
from scipy.cluster.hierarchy import dendrogram, linkage
from scipy.spatial.distance import pdist

# Create 5 points with labels (same as before)
points = {
    'A': (1.2, 5.2),
    'B': (2.7, 4.2),
    'C': (2, 6),
    'D': (5, 3),
    'E': (4, 2)
}

# Create figure with two subplots
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(6, 3))

# First subplot: Scatter plot with clusters
for label, (x, y) in points.items():
    ax1.scatter(x, y, s=100, alpha=0.7)
    ax1.annotate(label, (x, y), xytext=(5, 5), textcoords='offset points', 
                fontsize=12, fontweight='bold')

# Draw an ellipse around points A and C where A and C are the foci
A_x, A_y = points['A']
C_x, C_y = points['C']

# Calculate the distance between foci (A and C)
focal_distance = np.sqrt((C_x - A_x)**2 + (C_y - A_y)**2)

# Calculate center of ellipse (midpoint between foci)
center_x = (A_x + C_x) / 2
center_y = (A_y + C_y) / 2

# Calculate the angle of the major axis
angle = np.degrees(np.arctan2(C_y - A_y, C_x - A_x))

# Set semi-major axis (a) and semi-minor axis (b)
a = focal_distance/2 + 0.4  # semi-major axis with padding
c = focal_distance/2  # half the focal distance
b = np.sqrt(a**2 - c**2)  # semi-minor axis

# Create and add the ellipse for A and C
ellipse1 = Ellipse((center_x, center_y), 2*a, 2*b, angle=angle,
                   facecolor='none', edgecolor='red', linewidth=2, linestyle='--')
ax1.add_patch(ellipse1)

# Draw an ellipse around points E and D where E and D are the foci
E_x, E_y = points['E']
D_x, D_y = points['D']

# Calculate the distance between foci (E and D)
focal_distance_ED = np.sqrt((D_x - E_x)**2 + (D_y - E_y)**2)

# Calculate center of ellipse (midpoint between foci)
center_x_ED = (E_x + D_x) / 2
center_y_ED = (E_y + D_y) / 2

# Calculate the angle of the major axis
angle_ED = np.degrees(np.arctan2(D_y - E_y, D_x - E_x))

# Set semi-major axis (a) and semi-minor axis (b)
a_ED = focal_distance_ED/2 + 0.4  # semi-major axis with padding
c_ED = focal_distance_ED/2  # half the focal distance
b_ED = np.sqrt(a_ED**2 - c_ED**2)  # semi-minor axis

# Create and add the ellipse for E and D
ellipse2 = Ellipse((center_x_ED, center_y_ED), 2*a_ED, 2*b_ED, angle=angle_ED,
                   facecolor='none', edgecolor='blue', linewidth=2, linestyle='--')
ax1.add_patch(ellipse2)

# Draw a circle around points A, B, and C
A_x, A_y = points['A']
B_x, B_y = points['B']
C_x, C_y = points['C']

# Calculate the center of the circle (centroid of the three points)
center_x_ABC = (A_x + B_x + C_x) / 3
center_y_ABC = (A_y + B_y + C_y) / 3

# Calculate the radius as the maximum distance from center to any of the three points
dist_A = np.sqrt((A_x - center_x_ABC)**2 + (A_y - center_y_ABC)**2)
dist_B = np.sqrt((B_x - center_x_ABC)**2 + (B_y - center_y_ABC)**2)
dist_C = np.sqrt((C_x - center_x_ABC)**2 + (C_y - center_y_ABC)**2)
radius_ABC = max(dist_A, dist_B, dist_C) + 0.3  # Add some padding

# Create and add the circle
circle = plt.Circle((center_x_ABC, center_y_ABC), radius_ABC,
                   facecolor='none', edgecolor='green', linewidth=2, linestyle='--')
ax1.add_patch(circle)

# Draw an ellipse around all 5 points
all_x = [points[label][0] for label in points.keys()]
all_y = [points[label][1] for label in points.keys()]

# Calculate center of ellipse (centroid of all points)
center_x_all = np.mean(all_x)
center_y_all = np.mean(all_y)

width_all, height_all = 3.2, 7
angle_all = 40

# Create and add the ellipse around all points
ellipse_all = Ellipse((center_x_all, center_y_all), width_all, height_all, angle=angle_all,
                     facecolor='none', edgecolor='purple', linewidth=3, linestyle='-')
ax1.add_patch(ellipse_all)

ax1.set_xlabel('Feature 1')
ax1.set_ylabel('Feature 2')
ax1.set_title('Clusters at Different Levels')
ax1.grid(True, alpha=0.3)
ax1.set_xlim(0, 7)
ax1.set_ylim(0, 7)

# Second subplot: Dendrogram
# Prepare data for hierarchical clustering
points_array = np.array(list(points.values()))
point_labels = list(points.keys())

# Calculate linkage matrix
linkage_matrix = linkage(points_array, method='ward')

# Create dendrogram
dendrogram(linkage_matrix, labels=point_labels, ax=ax2, 
          leaf_rotation=0, leaf_font_size=12)
ax2.set_title('Dendrogram with Splits')
ax2.set_xlabel('Points')
ax2.set_ylabel('Distance')

# Add horizontal dashed red line at y=4 to show split level
ax2.axhline(y=4, color='red', linestyle='--', linewidth=2, alpha=0.8)

plt.tight_layout()

# Save the plot as a png image (uncomment to save)
# plt.savefig('figs/L08-dendrogram.png')
plt.show()

We can now split the dendrogram at a certain level to get a clustering

Hierarchical Clustering

A hierarchical clustering produces a set of nested clusters organized into a tree.

A hierarchical clustering is visualized using a dendrogram

A tree-like diagram that records the containment relations among clusters.

Strengths of Hierarchical Clustering

Hierarchical clustering has a number of advantages:

Encodes many different clusterings.
- It does not itself decide on the correct number of clusters.
A clustering is obtained by “cutting” the dendrogram at some level.
You can make this crucial decision yourself, by inspecting the dendrogram.
You can obtain a (somewhat) arbitrary number of clusters.

Another advantage

Another advantage is that the dendrogram may itself correspond to a meaningful structure, for example, a taxonomy.

Yet another advantage

Many hierarchical clustering methods can be performed using either similarity (proximity) or dissimilarity (distance) metrics.
This can be very helpful!
Techniques like \(k\)-means rely on a specific way of measuring similarity or distance between data points.

Compared to \(k\)-means

Another aspect of hierachical clustering is that it can handle certain cases better than \(k\)-means.

Because of the nature of the \(k\)-means algorithm, \(k\)-means tends to produce:

Roughly spherical clusters
Clusters of approximately equal size
Non-overlapping clusters

In many real-world situations, clusters may not be round, they may be of unequal size, and they may overlap.

Hence we would like clustering algorithms that can work in those cases also.

In-Class Exercise

Create a hierarchical cluster and dendogram for this data.

Code

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Ellipse
from scipy.cluster.hierarchy import dendrogram, linkage
from scipy.spatial.distance import pdist

# Create 5 points with labels (same as before)
points = {
    'A': (3.4, 6.1),
    'B': (1.8, 2.3),
    'C': (4.6, 4.9),
    'D': (1.6, 5.6),
    'E': (2.9, 1.7)
}

# Create figure with two subplots
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))

# First subplot: Scatter plot with clusters
for label, (x, y) in points.items():
    ax1.scatter(x, y, s=100, alpha=0.7)
    ax1.annotate(label, (x, y), xytext=(5, 5), textcoords='offset points', 
                fontsize=12, fontweight='bold')


ax1.set_xlabel('Feature 1')
ax1.set_ylabel('Feature 2')
ax1.set_title('Clusters at Different Levels')
ax1.grid(True, alpha=0.3)
ax1.set_xlim(0, 7)
ax1.set_ylim(0, 7)

# Create empty axis with 5 evenly spaced ticks
ax2.set_xlim(0, 4)
ax2.set_ylim(0, 1)
ax2.set_xticks([0, 1, 2, 3, 4])
ax2.set_xticklabels([])
ax2.set_yticks([0, 0.25, 0.5, 0.75, 1])
ax2.set_yticklabels([])
ax2.set_title('Dendogram')
ax2.set_xlabel('Points')
ax2.set_ylabel('Distance')

plt.tight_layout()

# Save the plot as a png image (uncomment to save)
# plt.savefig('figs/L08-dendrogram.png')
plt.show()

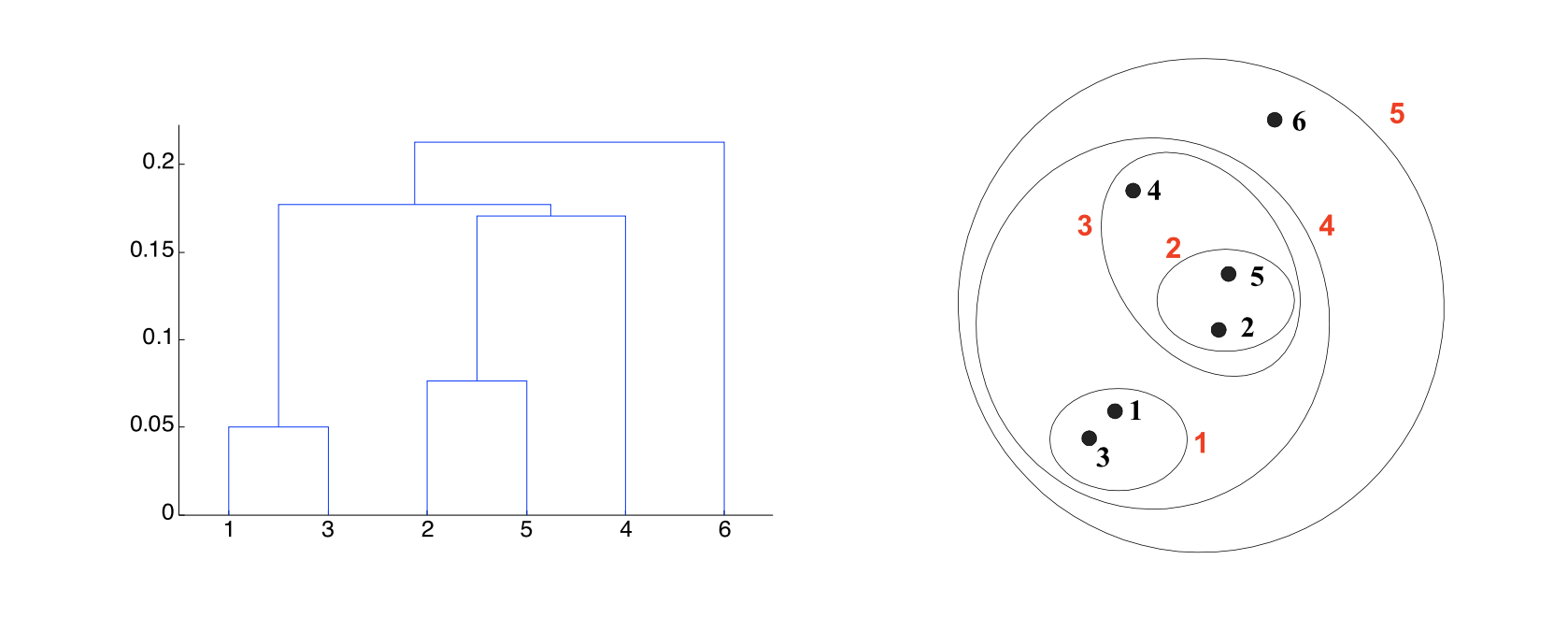
Hierarchical Clustering Algorithms

There are two main approaches to hierarchical clustering: “bottom-up” and “top-down.”

Agglomerative Clustering (“bottom-up”):

Start by defining each point as its own cluster
At each successive step, merge the two clusters that are closest to each other
Repeat until only one cluster is left.

Divisive Clustering (“top-down”):

Start with one, all-inclusive cluster
At each step, find the cluster split that creates the largest distance between resulting clusters
Repeat until each point is in its own cluster.

Some key points

Agglomerative techniques are by far the more common.
The key to both of these methods is defining the distance between two clusters.
Different definitions for the inter-cluster distance yield different clusterings.

To illustrate the impact of the choice of cluster distances, we’ll focus on agglomerative clustering.

Hierarchical Clustering Algorithm Inputs

Input data as either
- 2-D sample/feature matrix
- 1D condensed distance matrix – upper triangular of pairwise distance matrix flattened
The cluster linkage method (single, complete, average, ward, …)
The distance metric (Euclidean, manhattan, Jaccard, …)

Hierarchical Clustering Algorithm Output

An \((n-1,4)\) shaped linkage matrix.

Where each row is [idx1, idx2, dist, sample_count] is a single step in the clustering process and

idx1 and idx2 are indices of the cluster being merged, where

indices \(\{ 0...n-1 \}\) refer to the original data points and
indices \(\{n, n+1, ...\}\) refer to each new cluster created

And sample_count is the number of original data samples in the new cluster.

Linkage Matrix Example

Let’s calculate and display the linkage matrix for our 5 data points A-E:

Code

# Create 5 points with labels (same as before)
points = {
    'A': (1.2, 5.2),
    'B': (2.7, 4.2),
    'C': (2, 6),
    'D': (5, 3),
    'E': (4, 2)
}

# Prepare data for hierarchical clustering
points_array = np.array(list(points.values()))
point_labels = list(points.keys())

# Calculate linkage matrix using Ward's method
linkage_matrix = linkage(points_array, method='ward')

print("Linkage Matrix for 5 data points A-E:")
print("Format: [idx1, idx2, distance, sample_count]")
print("=" * 50)
print(linkage_matrix)
print("=" * 50)

# Display with labels for better understanding
print("\nInterpretation:")
print(f"Row 0: Merge points 0 and 2 (A and C) at distance {linkage_matrix[0,2]:.2f}")
print(f"Row 1: Merge points 3 and 4 (D and E) at distance {linkage_matrix[1,2]:.2f}") 
print(f"Row 2: Merge point 1 (B) with cluster 5 (A&C) at distance {linkage_matrix[2,2]:.2f}")
print(f"Row 3: Merge cluster 6 (A&B&C) with cluster 7 (D&E) at distance {linkage_matrix[3,2]:.2f}")

Linkage Matrix for 5 data points A-E:
Format: [idx1, idx2, distance, sample_count]
==================================================
[[0.         2.         1.13137085 2.        ]
 [3.         4.         1.41421356 2.        ]
 [1.         5.         2.05588586 3.        ]
 [6.         7.         5.66085977 5.        ]]
==================================================

Interpretation:
Row 0: Merge points 0 and 2 (A and C) at distance 1.13
Row 1: Merge points 3 and 4 (D and E) at distance 1.41
Row 2: Merge point 1 (B) with cluster 5 (A&C) at distance 2.06
Row 3: Merge cluster 6 (A&B&C) with cluster 7 (D&E) at distance 5.66

Hierarchical Clustering Algorithm Explained

Initialization
- Start with each data point as its own cluster.
- Calculate the distance matrix if not provided
Iterative Clustering
- At each step, the two closest clusters (according to linkage method and distance metric) are merged into a new cluster.
- The distance between new cluster and the remaining clusters is added
- Repeat previous two steps until only one cluster remains.

Defining Cluster Proximity

Given two clusters, how do we define the distance between them?

Here are three natural ways to do it.

Cluster Proximity – Single-Linkage

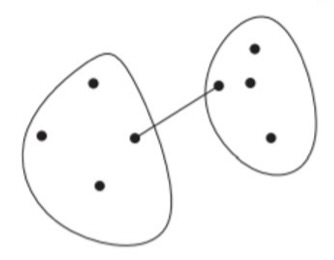
Single-Linkage: the distance between two clusters is the distance between the closest two points that are in different clusters.

\[ D_\text{single}(i,j) = \min_{x, y}\{d(x, y) \,|\, x \in C_i, y \in C_j\} \]

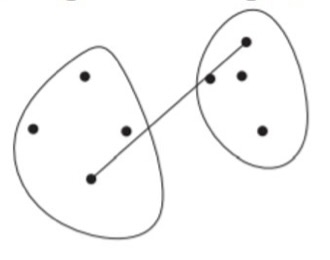
Cluster Proximity – Complete-Linkage

Complete-Linkage: the distance between two clusters is the distance between the farthest two points that are in different clusters.

\[ D_\text{complete}(i,j) = \max_{x, y}\{d(x, y) \,|\, x \in C_i, y \in C_j\} \]

Cluster Proximity – Average-Linkage

Average-Linkage: the distance between two clusters is the average distance between all pairs of points from different clusters.

\[ D_\text{average}(i,j) = \frac{1}{|C_i|\cdot|C_j|}\sum_{x \in C_i,\, y \in C_j}d(x, y) \]

Cluster Proximity Example

Notice that it is easy to express the definitions above in terms of similarity instead of distance.

Here is a set of 6 points that we will cluster to show differences between distance metrics.

Code

plt.figure(figsize=(6,4))
pt_x = [0.4, 0.22, 0.35, 0.26, 0.08, 0.45]
pt_y = [0.53, 0.38, 0.32, 0.19, 0.41, 0.30]
plt.plot(pt_x, pt_y, 'o', markersize = 10, color = 'k')
plt.ylim([.15, .60])
plt.xlim([0.05, 0.70])
for i in range(6):
    plt.annotate(f'{i}', (pt_x[i]+0.02, pt_y[i]-0.01), fontsize = 12)
plt.axis('on')
plt.xticks([])
plt.yticks([])
plt.show()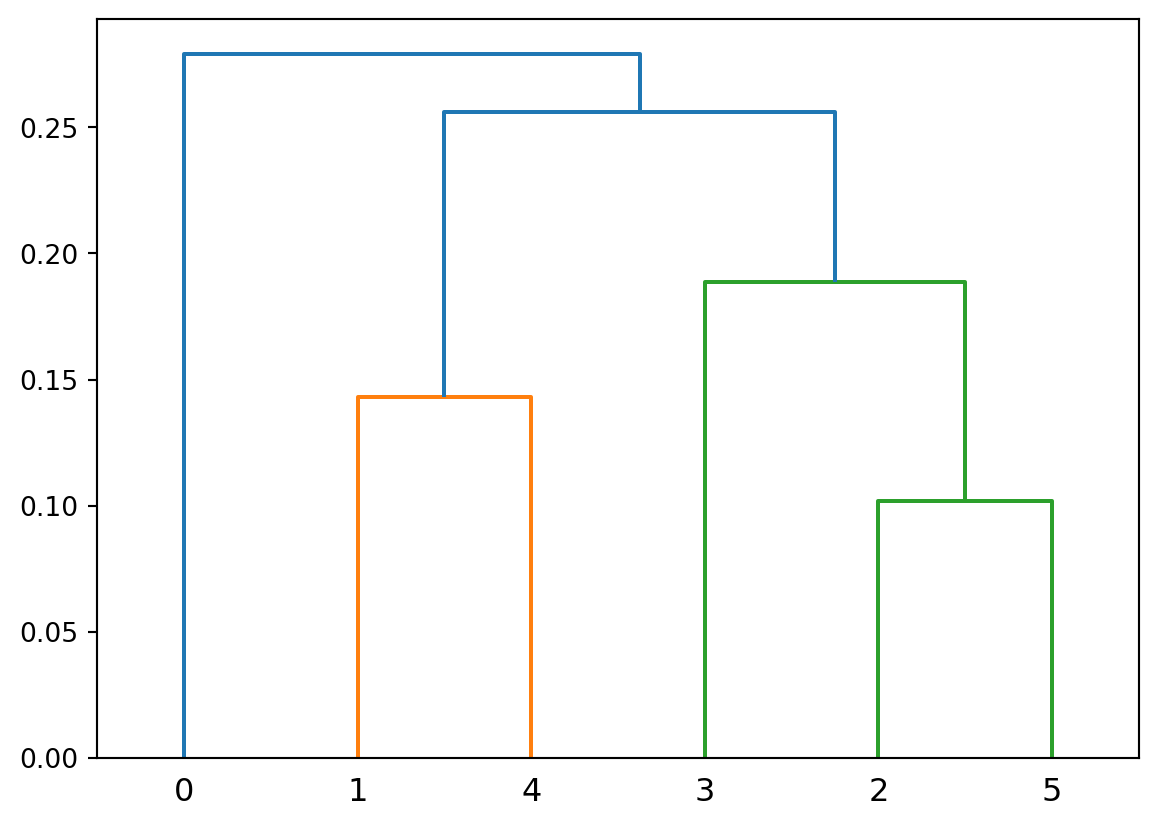

We can calculate the distance matrix

Code

X = np.array([pt_x, pt_y]).T
from scipy.spatial import distance_matrix
labels = ['p0', 'p1', 'p2', 'p3', 'p4', 'p5']
D = pd.DataFrame(distance_matrix(X, X), index = labels, columns = labels)
D.style.format('{:.2f}')

	p0	p1	p2	p3	p4	p5
p0	0.00	0.23	0.22	0.37	0.34	0.24
p1	0.23	0.00	0.14	0.19	0.14	0.24
p2	0.22	0.14	0.00	0.16	0.28	0.10
p3	0.37	0.19	0.16	0.00	0.28	0.22
p4	0.34	0.14	0.28	0.28	0.00	0.39
p5	0.24	0.24	0.10	0.22	0.39	0.00

Single-Linkage Clustering

Code

import scipy.cluster
import scipy.cluster.hierarchy as hierarchy
Z = hierarchy.linkage(X, method='single', metric='euclidean')
hierarchy.dendrogram(Z)
plt.show()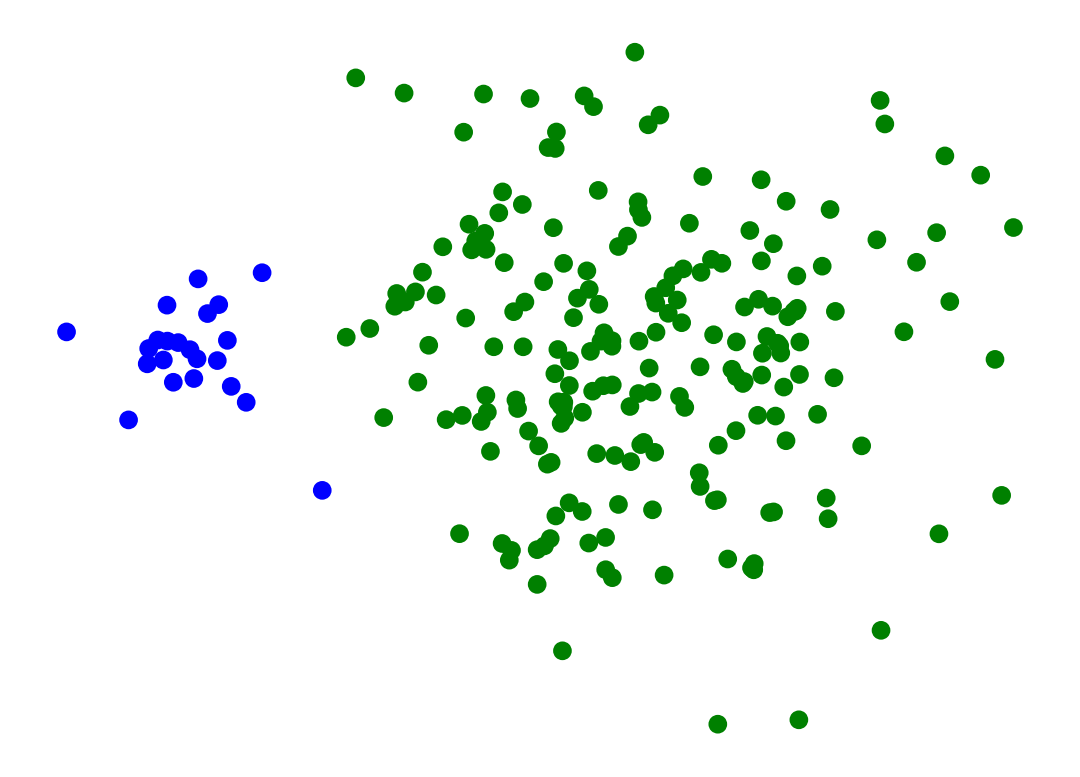

Single Linkage Clustering Advantages

Single-linkage clustering can handle non-elliptical shapes.

Here we use SciPy’s fcluster to form flat custers from hierarchical clustering.

Code

X_moon_05, y_moon_05 = sk_data.make_moons(random_state = 0, noise = 0.05)

Z = hierarchy.linkage(X_moon_05, method='single')
labels = hierarchy.fcluster(Z, 2, criterion = 'maxclust')

plt.scatter(X_moon_05[:, 0], X_moon_05[:, 1], c = [['b','g'][i-1] for i in labels])
plt.axis('off')
plt.show()

Single-Linkage can find different sized clusters:

Code

X_rand_lo, y_rand_lo = sk_data.make_blobs(n_samples=[20, 200], centers = [[1, 1], [3, 1]], n_features = 2,
                          center_box = (-10.0, 10.0), cluster_std = [.1, .5], random_state = 0)

Z = hierarchy.linkage(X_rand_lo, method='single')
labels = hierarchy.fcluster(Z, 2, criterion = 'maxclust')

plt.scatter(X_rand_lo[:, 0], X_rand_lo[:, 1], c = [['b','g'][i-1] for i in labels])
# plt.title('Single-Linkage Can Find Different-Sized Clusters')
plt.axis('off')
plt.show()

Single Linkage Disadvantages

Single-linkage clustering can be sensitive to noise and outliers.

The results can change drastically on even slightly more noisy data.

Code

X_moon_10, y_moon_10 = sk_data.make_moons(random_state = 0, noise = 0.1)

Z = hierarchy.linkage(X_moon_10, method='single')
labels = hierarchy.fcluster(Z, 2, criterion = 'maxclust')

plt.scatter(X_moon_10[:, 0], X_moon_10[:, 1], c = [['b','g'][i-1] for i in labels])
# plt.title('Single-Linkage Clustering Changes Drastically on Slightly More Noisy Data')
plt.axis('off')
plt.show()

And here’s another example where we bump the standard deviation on the clusters slightly.

Code

X_rand_hi, y_rand_hi = sk_data.make_blobs(n_samples=[20, 200], centers = [[1, 1], [3, 1]], n_features = 2,
                          center_box = (-10.0, 10.0), cluster_std = [.15, .6], random_state = 0)

Z = hierarchy.linkage(X_rand_hi, method='single')
labels = hierarchy.fcluster(Z, 2, criterion = 'maxclust')

plt.scatter(X_rand_hi[:, 0], X_rand_hi[:, 1], c = [['b','g'][i-1] for i in labels])
plt.axis('off')
plt.show()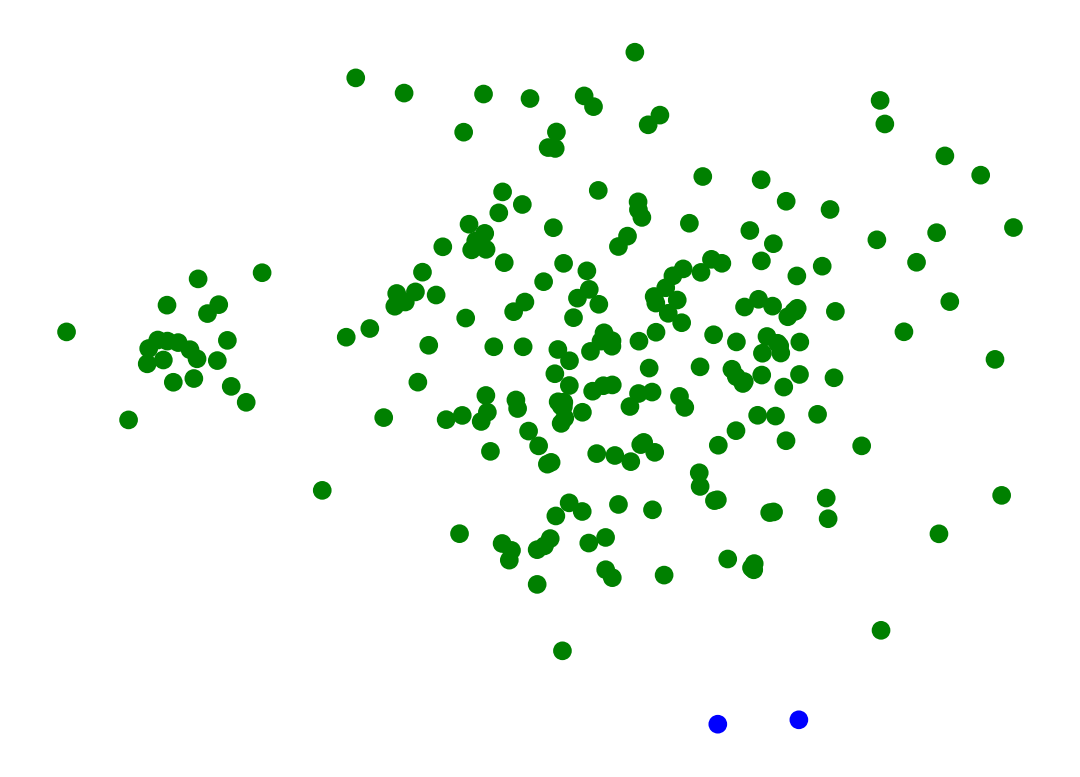

Complete-Linkage Clustering

Code

Z = hierarchy.linkage(X, method='complete')
hierarchy.dendrogram(Z)
plt.show()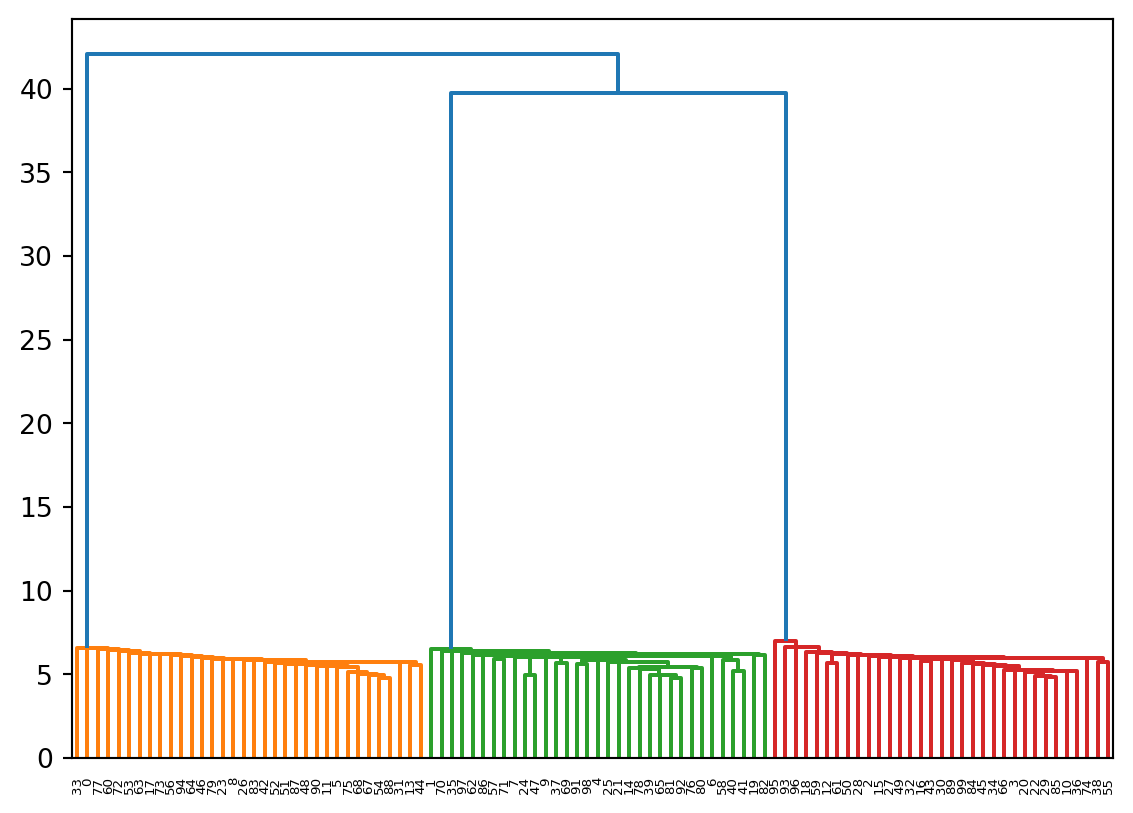

Complete-Linkage Clustering Advantages

Produces more-balanced clusters – more-equal diameters

Code

X_moon_05, y_moon_05 = sk_data.make_moons(random_state = 0, noise = 0.05)

Z = hierarchy.linkage(X_moon_05, method='complete')
labels = hierarchy.fcluster(Z, 2, criterion = 'maxclust')

plt.scatter(X_moon_05[:, 0], X_moon_05[:, 1], c = [['b','g'][i-1] for i in labels])
plt.axis('off')
plt.show()

Code

Z = hierarchy.linkage(X_rand_hi, method='complete')
labels = hierarchy.fcluster(Z, 2, criterion = 'maxclust')

plt.scatter(X_rand_hi[:, 0], X_rand_hi[:, 1], c = [['b','g'][i-1] for i in labels])
plt.axis('off')
plt.show()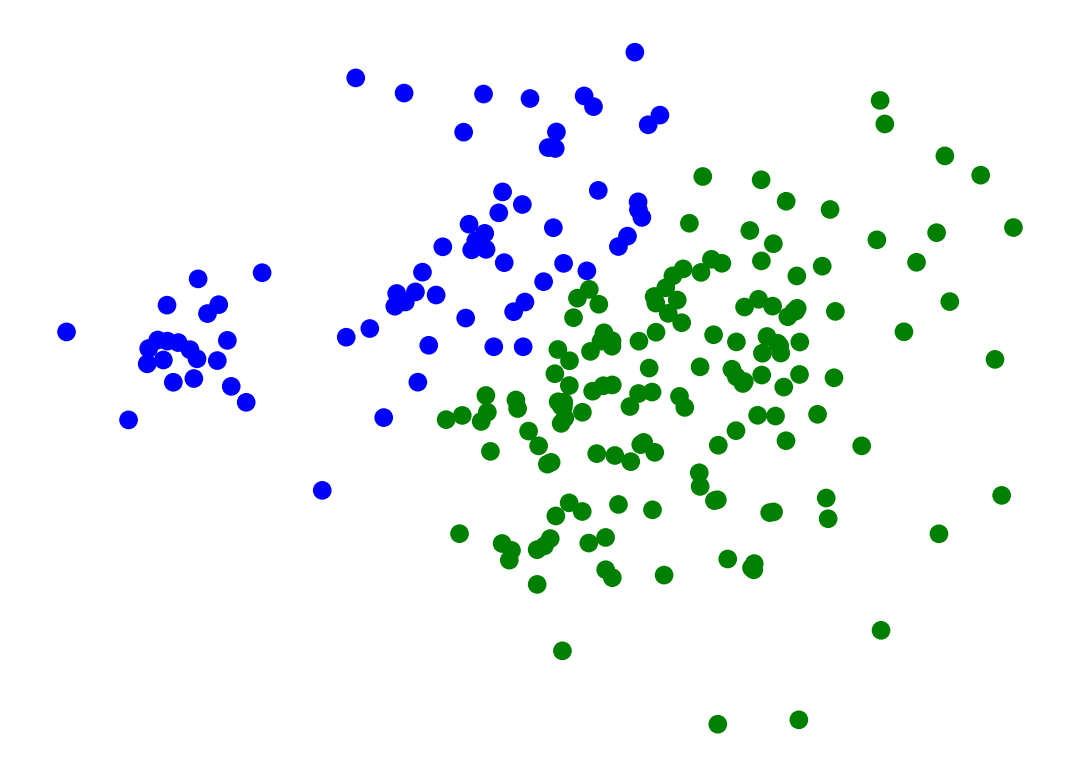

Less susceptible to noise:

Code

Z = hierarchy.linkage(X_moon_10, method='complete')
labels = hierarchy.fcluster(Z, 2, criterion = 'maxclust')
plt.scatter(X_moon_10[:, 0], X_moon_10[:, 1], c = [['b','g'][i-1] for i in labels])

plt.axis('off')
plt.show()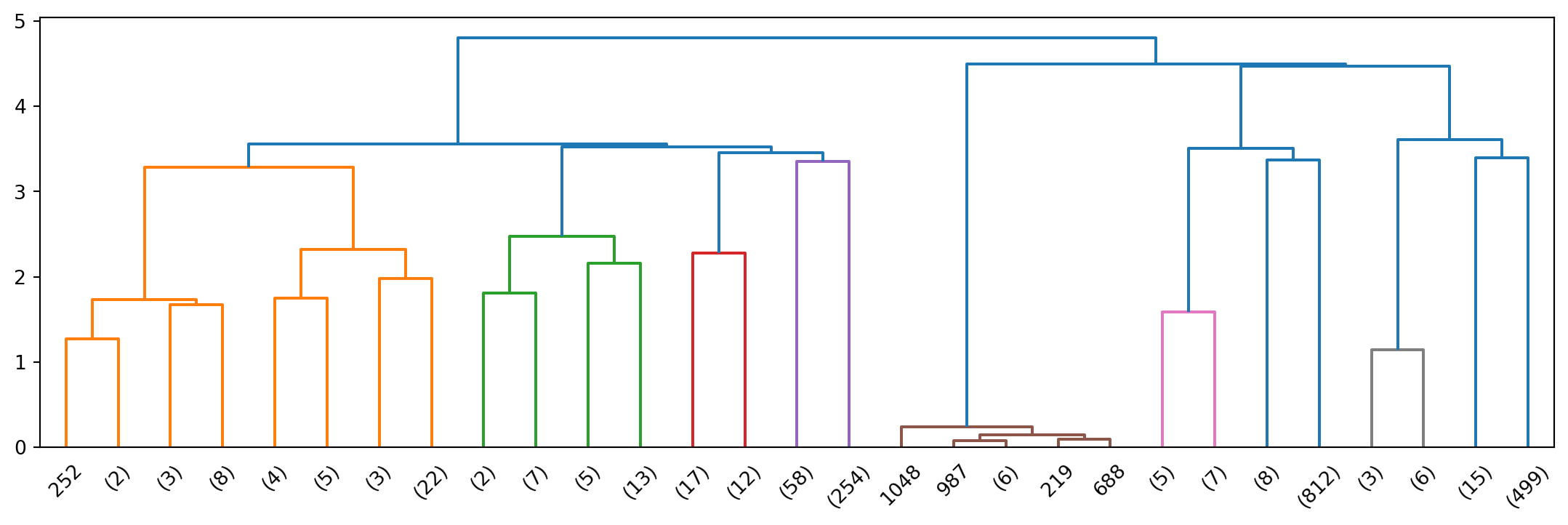

Complete-Linkage Clustering Disadvantages

Some disadvantages for complete-linkage clustering are:

Sensitivity to outliers
Tendency to compute more compact, spherical clusters
Computationally intensive for large datasets.

Average-Linkage Clustering

Code

Z = hierarchy.linkage(X, method='average')
hierarchy.dendrogram(Z)
plt.show()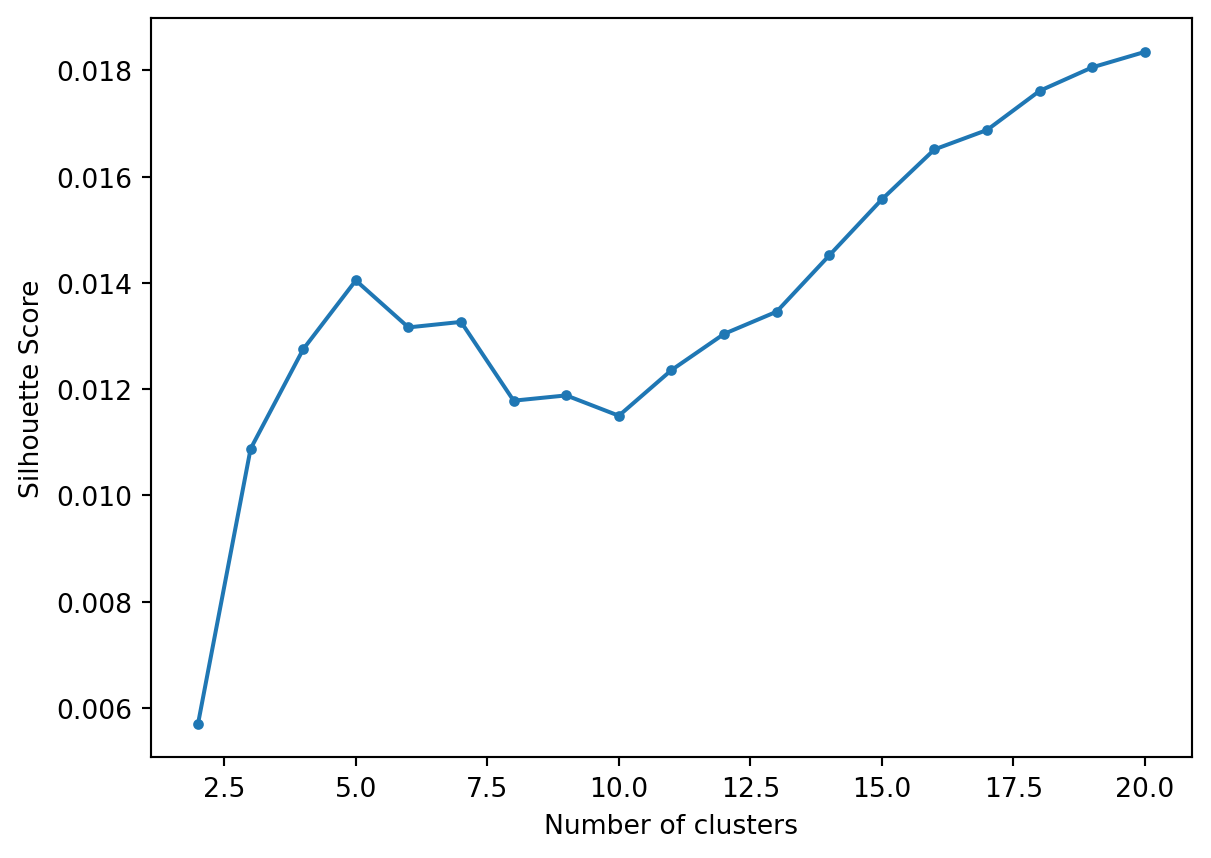

Average-Linkage Clustering Strengths and Limitations

Average-Linkage clustering is in some sense a compromise between Single-linkage and Complete-linkage clustering.

Strengths:

Less susceptible to noise and outliers

Limitations:

Biased toward elliptical clusters

Average-Linkage Clustering Strengths and Limitations, cont.

Produces more isotropic clusters.

Code

Z = hierarchy.linkage(X_moon_10, method='average')
labels = hierarchy.fcluster(Z, 2, criterion = 'maxclust')
plt.scatter(X_moon_10[:, 0], X_moon_10[:, 1], c = [['b','g'][i-1] for i in labels])

plt.axis('off')
plt.show()

Average-Linkage Clustering Strengths and Limitations, cont.

More resistant to noise than Single-Linkage.

Code

Z = hierarchy.linkage(X_rand_hi, method='average')
labels = hierarchy.fcluster(Z, 2, criterion = 'maxclust')
plt.scatter(X_rand_hi[:, 0], X_rand_hi[:, 1], c = [['b','g'][i-1] for i in labels])

plt.axis('off')
plt.show()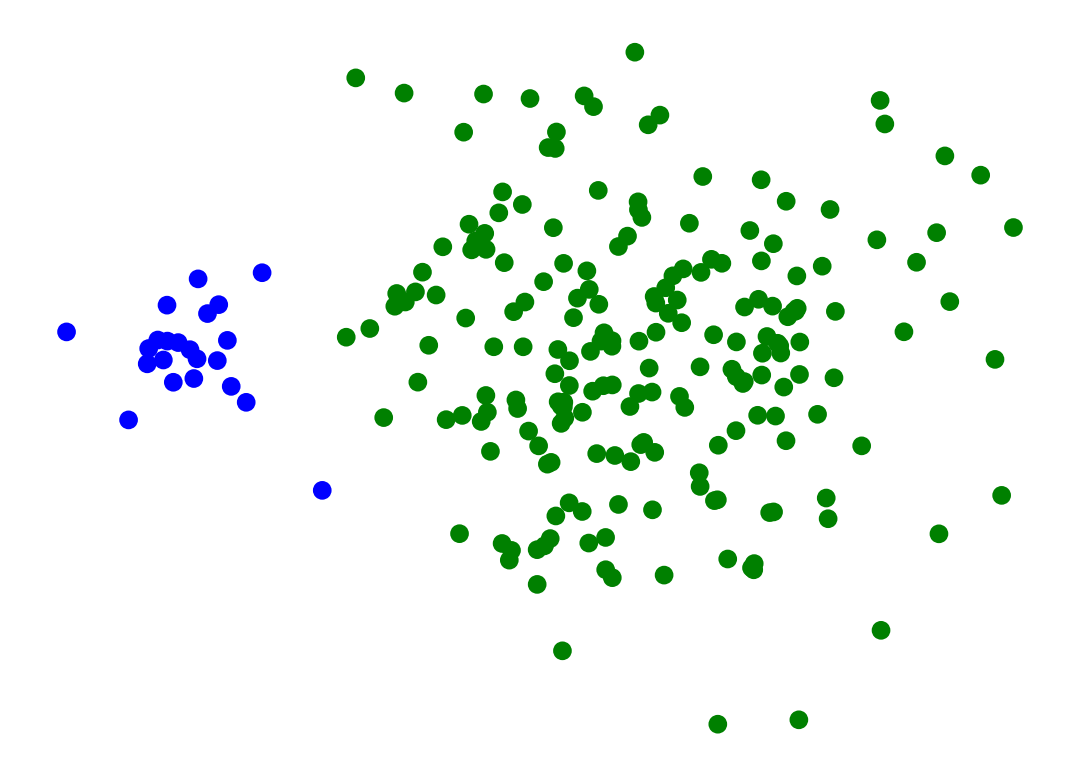

All Three Compared

Ward’s Distance

Finally, we consider one more cluster distance.

Ward’s distance asks “What if we combined these two clusters – how would clustering improve?”

To define “how would clustering improve?” we appeal to the \(k\)-means criterion.

So:

Ward’s Distance between clusters \(C_i\) and \(C_j\) is the difference between the total within cluster sum of squares for the two clusters separately, compared to the within cluster sum of squares resulting from merging the two clusters into a new cluster \(C_{i+j}\):

\[ D_\text{Ward}(i, j) = \sum_{x \in C_i} (x - c_i)^2 + \sum_{x \in C_j} (x - c_j)^2 - \sum_{x \in C_{i+j}} (x - c_{i+j})^2 \]

where \(c_i, c_j, c_{i+j}\) are the corresponding cluster centroids.

Ward’s Distance continued

In a sense, this cluster distance results in a hierarchical analog of \(k\)-means.

As a result, it has properties similar to \(k\)-means:

Less susceptible to noise and outliers
Biased toward elliptical clusters

Hence it tends to behave more like average-linkage hierarchical clustering.

Hierarchical Clustering in Practice

In Practice

Now we’ll look at doing hierarchical clustering in practice.

We’ll use 1/10th of the synthetic data set from the beginning of this lecture.

scipy has a comprehensive set of clustering tools.

Code

X, y = sk_data.make_blobs(
    n_samples=[10, 10, 25, 7, 7, 8], 
    centers = [[1, 2], [1.5, 1], [3, 2], [1.75, 3.25], [2, 4], [2.25, 3.25]], 
    n_features = 2,
    center_box = (-10.0, 10.0), 
    cluster_std = [.2, .2, .3, .1, .15, .15], 
    random_state = 0
)

df_rand = pd.DataFrame(np.column_stack([X[:, 0], X[:, 1], y]), columns = ['X', 'Y', 'label'])

df_rand.plot('X', 'Y', kind = 'scatter',  
                   colorbar = False, figsize = (5, 5))
plt.axis('square')
plt.axis('off')
plt.show()

In Practice, cont.

Let’s run hierarchical clustering on our synthetic dataset.

Try the other linkage methods and see how the clustering and dendrogram changes.

# linkages = ['single','complete','average','weighted','ward']
Z = hierarchy.linkage(X, method = 'single')

And draw the dendrogram.

Code

R = hierarchy.dendrogram(Z)

Hierarchical Clustering – Newsgroups

Once again we’ll use the “20 Newsgroup” data provided as example data in sklearn. Experiment with different metrics.

Load three of the newsgroups.

Code

from sklearn.datasets import fetch_20newsgroups
categories = ['comp.os.ms-windows.misc', 'sci.space','rec.sport.baseball']
news_data = fetch_20newsgroups(subset = 'train', categories = categories)

Vectorize the data.

Code

from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer(stop_words='english', min_df = 4, max_df = 0.8)
data = vectorizer.fit_transform(news_data.data).todense()
data.shape

(1781, 9409)

Code

# linkages are one of 'single','complete','average','weighted','ward'
#
# metrics can be ‘braycurtis’, ‘canberra’, ‘chebyshev’, ‘cityblock’, ‘correlation’, ‘cosine’, 
# ‘dice’, ‘euclidean’, ‘hamming’, ‘jaccard’, ‘kulsinski’, ‘mahalanobis’, ‘matching’, 
# ‘minkowski’, ‘rogerstanimoto’, ‘russellrao’, ‘seuclidean’, ‘sokalmichener’, ‘sokalsneath’, 
# ‘sqeuclidean’, ‘yule’.

Z_20ng = hierarchy.linkage(data, method = 'ward', metric = 'euclidean')
plt.figure(figsize=(14,4))
R_20ng = hierarchy.dendrogram(Z_20ng, p=4, truncate_mode = 'level', show_leaf_counts=True)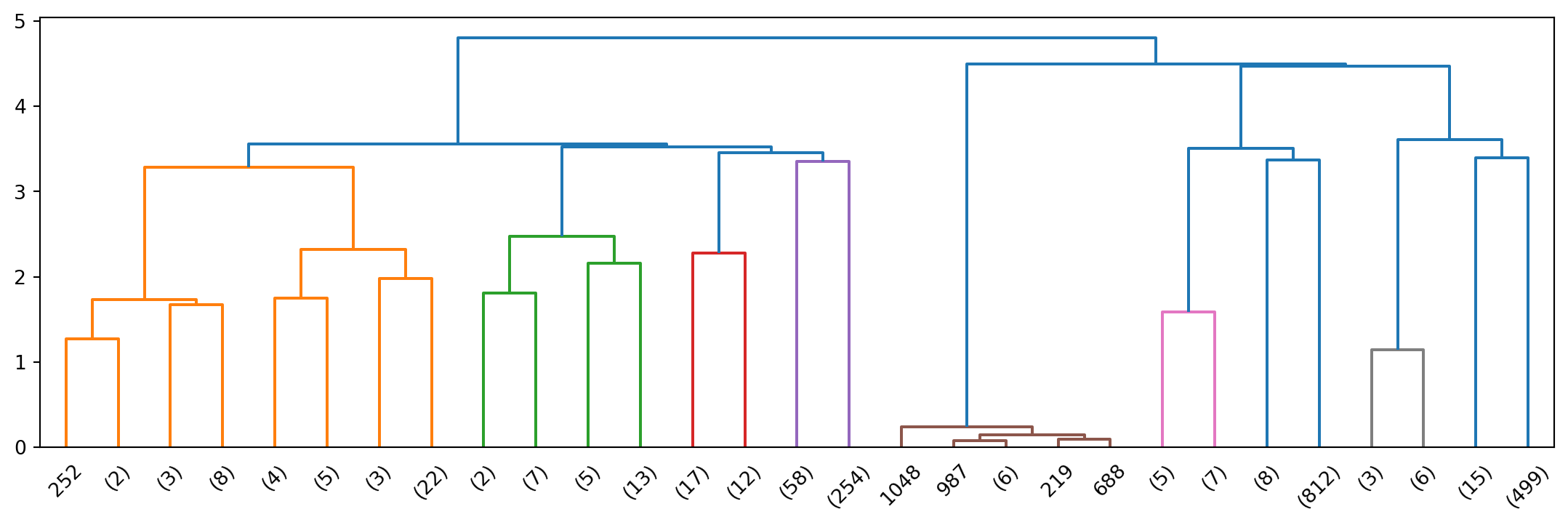

Selecting the Number of Clusters

Let’s flatten the hierarchy to different numbers clusters and calculate the Silhouette Score.

Code

import sklearn.metrics as metrics

max_clusters = 20
s = np.zeros(max_clusters+1)

for k in range(2, max_clusters+1):
    clusters = hierarchy.fcluster(Z_20ng, k, criterion = 'maxclust')
    s[k] = metrics.silhouette_score(np.asarray(data), clusters, metric = 'euclidean')

plt.plot(range(2, len(s)), s[2:], '.-')
plt.xlabel('Number of clusters')
plt.ylabel('Silhouette Score')
plt.show()

/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: divide by zero encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: overflow encountered in matmul
  ret = a @ b
/Users/tgardos/Source/courses/ds701/DS701-Course-Notes/.venv/lib/python3.10/site-packages/sklearn/utils/extmath.py:203: RuntimeWarning: invalid value encountered in matmul
  ret = a @ b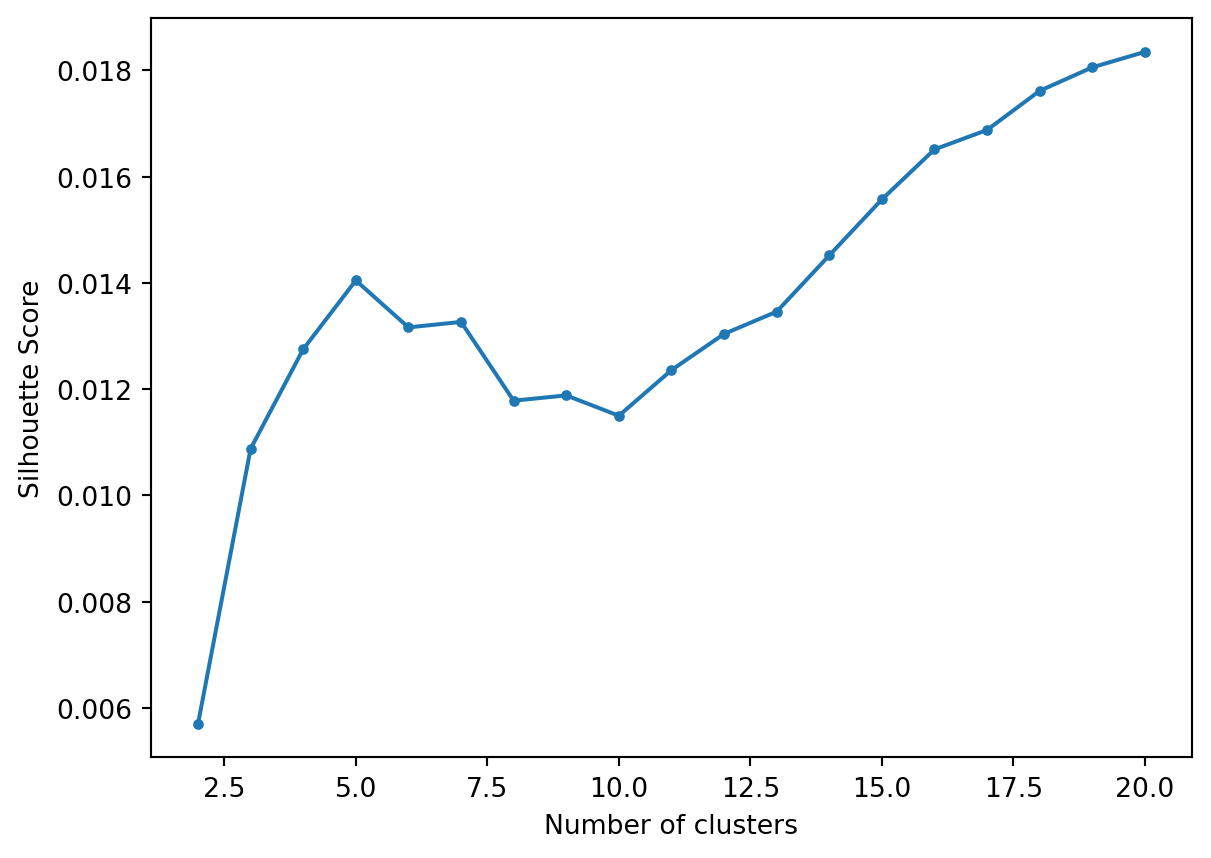

We see a first peak at 5.

Top terms per cluster when we flatten to a depth of 5.

Code

k = 5
clusters = hierarchy.fcluster(Z_20ng, k, criterion = 'maxclust')
for i in range(1,k+1):
    items = np.array([item for item,clust in zip(data, clusters) if clust == i])
    centroids = np.squeeze(items).mean(axis = 0)
    asc_order_centroids = centroids.argsort()#[:, ::-1]
    order_centroids = asc_order_centroids[::-1]
    terms = vectorizer.get_feature_names_out()
    print(f'Cluster {i}:')
    for ind in order_centroids[:10]:
        print(f' {terms[ind]}')
    print('')

Cluster 1:
 space
 nasa
 edu
 henry
 gov
 alaska
 access
 com
 moon
 digex

Cluster 2:
 ax
 max
 b8f
 g9v
 a86
 145
 1d9
 pl
 2di
 0t

Cluster 3:
 edu
 com
 year
 baseball
 article
 writes
 cs
 team
 game
 university

Cluster 4:
 risc
 instruction
 ghhwang
 csie
 set
 nctu
 cisc
 tw
 reduced
 mq

Cluster 5:
 windows
 edu
 file
 dos
 com
 files
 card
 drivers
 driver
 use

Comparison of Linkages

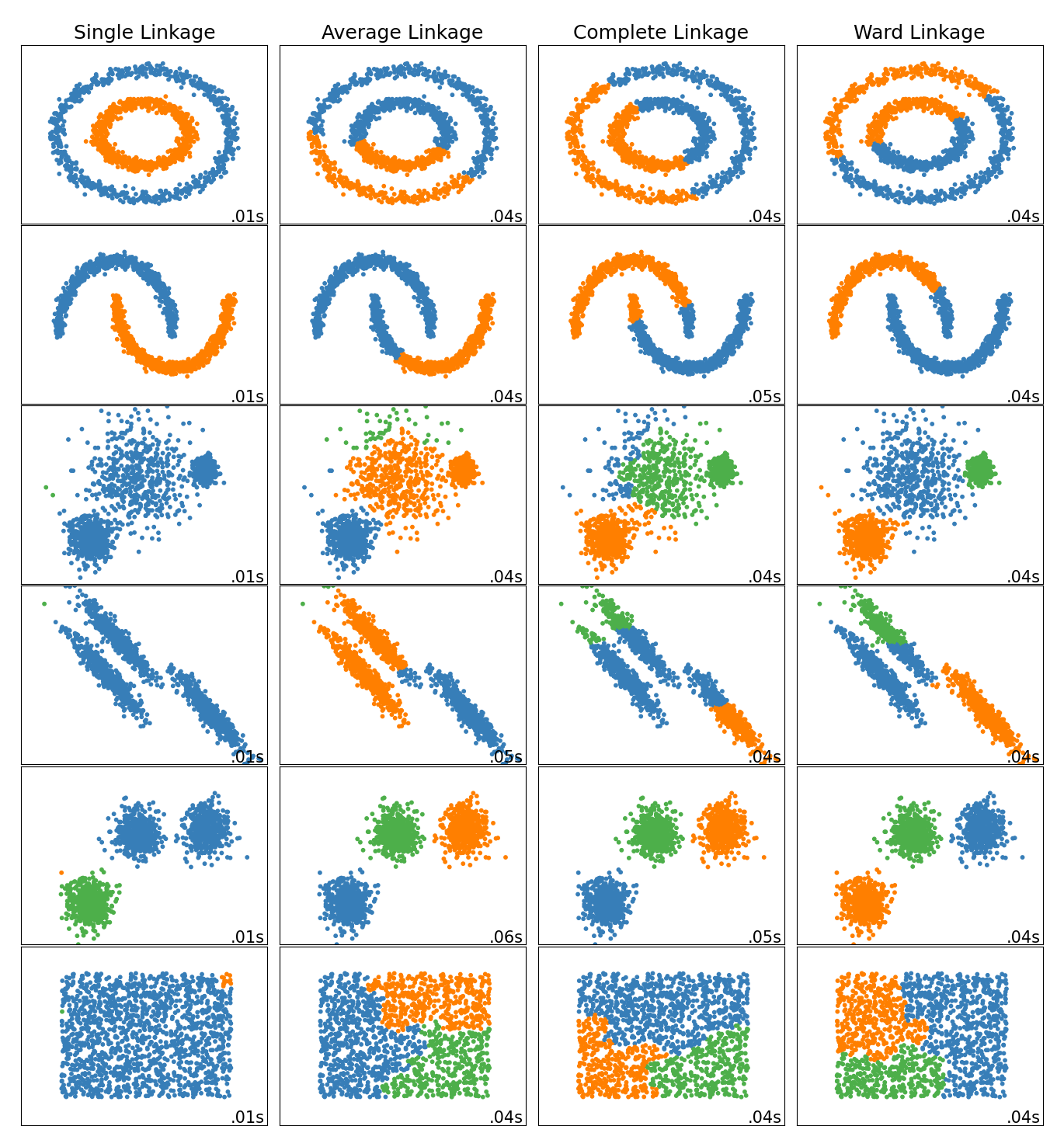
Scikit-Learn has a very nice notebook and plot, copied here, that shows the different clusters resulting from different linkage methods.

Recap

Clustering Recap

This wraps up our partitional Cluster topics. We covered:

What the clustering problem is
An overview of the \(k\)-means clustering algorithm including initialization with \(k\)-means++
Visualization techniques such as Multi-Dimensional Scaling
Cluster evaluation with (Adjusted) Rand Index and Silhouette Coefficient
Using evaluation to determine number of clusters
Hierarchical Clustering with different methods and metrics
Looked at applications of clustering on various types of synthetic data, image color quantization, newsgroup clustering