NN II – Compute Graph, Backprop and Training

Introduction

In this lecture we’ll gradually build out a light weight neural network training framework reminiscent of PyTorch.

We build:

A simple neural network engine we call Value class that wraps numbers and math operators and includes useful attributes and methods for implementing forward pass and back propagation. (~63 lines of code)

We’ll provide (and explain)

A simple compute graph visualization function. (34 lines of code)
A small set of helper functions that easily define a neuron, layer and multi-layer perceptron (MLP). (84 lines of code)

With that we can implement a neural network training loop, and see how similar it is to a PyTorch implementation.

The code is based on Andrej Karpathy’s micrograd.

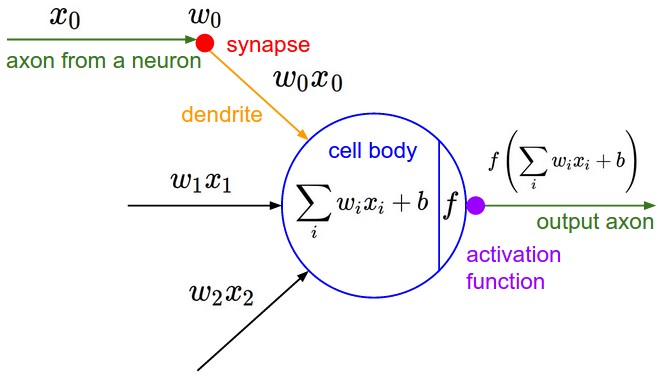
Artificial Neuron

Recall we looked at an artificial neuron in the Neural Networks I lecture.

From cs231n

The common artifical neuron

collects one or more inputs,
each multiplied by a unique weight
sums the weighted inputs
adds a bias
then applies a nonlinear activation function

Activation Functions

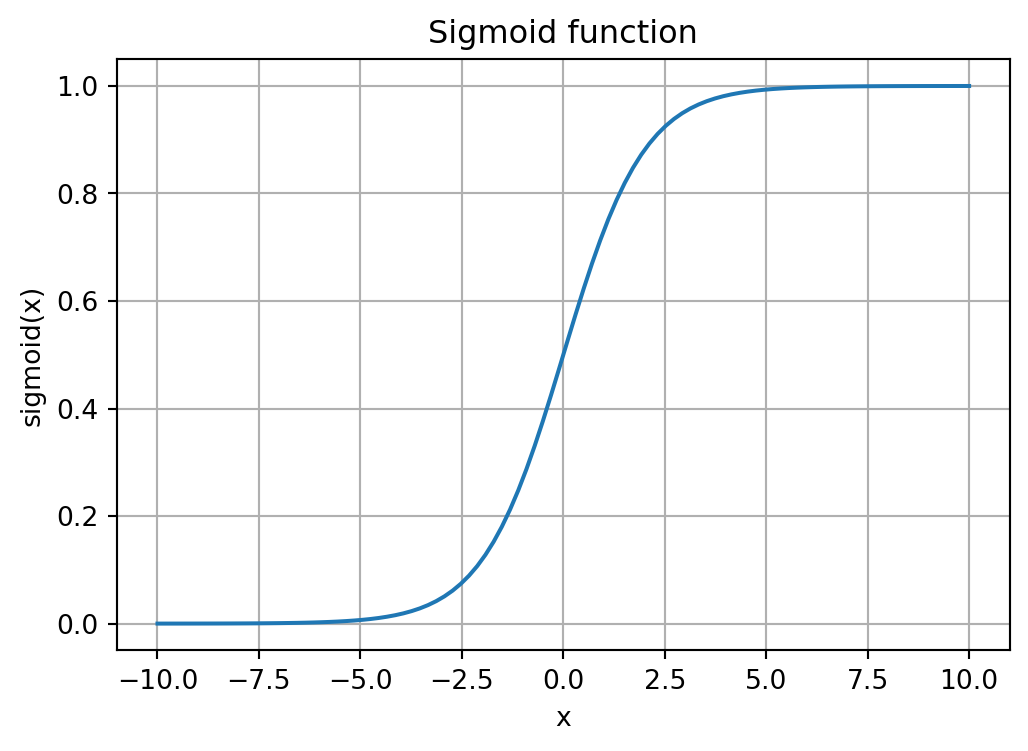
The activation function is typically some nonlinear function that compresses the input in some way. Historically, it’s been the sigmoid and \(\tanh()\) functions.

Important

Without a nonlinear activation function, a neural network collapses to just a linear model and loses all its expressive power. To dive deeper, see the Universal Approximation Theorem in Chapter 3 of Understanding Deep Learning.

The sigmoid function is

\[ \mathrm{sigmoid}(x) = \frac{1}{1 + e^{-x}}. \]

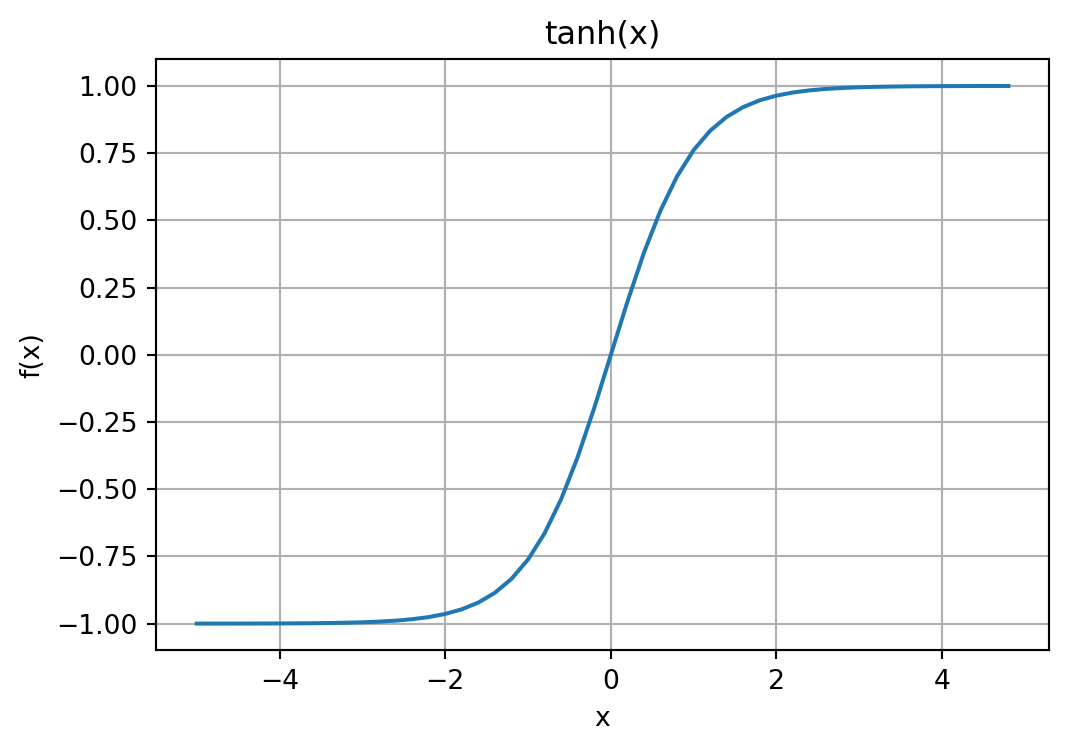
The hyperbolic tangent, \(\tanh\), is basically the sigmoid function shifted and scaled to a range of [-1,1]. The tanh function is

\[ \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}. \]

A more common activation function these days and that is more efficient to implement is the Rectified Linear Unit or ReLU.

\[ \textrm{ReLU}(x) = \mathrm{max}(0, x) \]

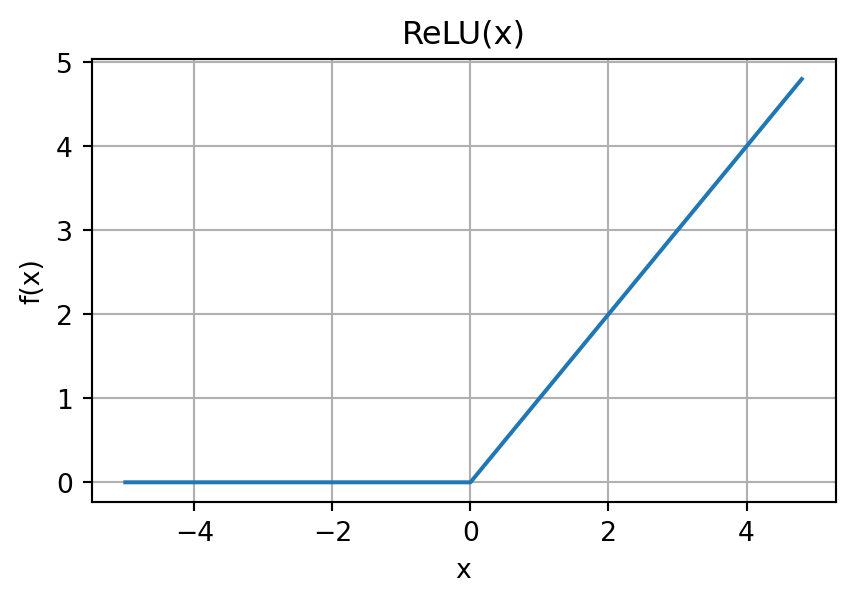
There are many other variations. See for example PyTorch Non-linear Activations.

Relating Back to an Earlier Lecture

Question

What does

\[ \mathrm{sigmoid}\left(\sum_i w_i x_i + b\right) \hspace{10pt} \textrm{where} \hspace{10pt} \mathrm{sigmoid}(x) = \frac{1}{1 + e^{-x}} \]

remind you of?

Answer

How about the Logistic Regression model?

In fact, just like in Logistic Regression, we use the sigmoid function on the last layer of a neural network that is doing binary classification to output the probabilities.

So Logistic Regression is similar to one neuron with a sigmoid activation function.

Fully Connected Network (FCN)

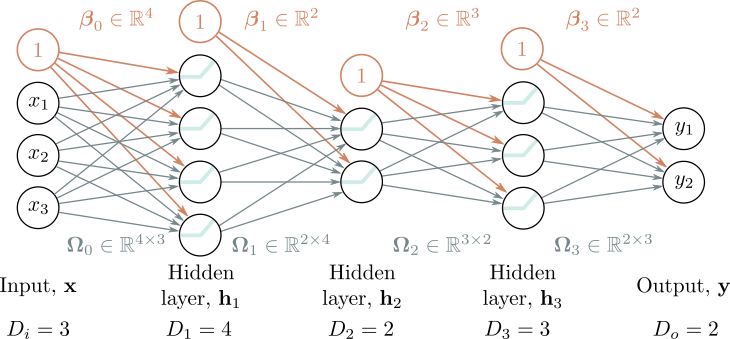
Layer: Multiple artificial neurons acting on the same inputs.
Network: Multiple cascading layers produce one or more outputs.

The above network has

3 inputs,
three hidden layers of 4, 2 and 3 neurons, respectively, followed by
one layer that produces two continuous value outputs.

This is a regression model that is predicting two continuous valued outputs.

FCN Matrix Equations

We can express the matrix equations for a \(K\) layer network as

\[ \begin{aligned} \mathbf{h}_1 &= \mathbf{a}(\boldsymbol{\beta}_0 + \boldsymbol{\Omega}_0 \mathbf{x}) \\ \mathbf{h}_2 &= \mathbf{a}(\boldsymbol{\beta}_1 + \boldsymbol{\Omega}_1 \mathbf{h}_1) \\ \vdots \\ \mathbf{h}_K &= \mathbf{a}(\boldsymbol{\beta}_{K-1} + \boldsymbol{\Omega}_{K-1} \mathbf{h}_{K-1}) \\ \mathbf{\hat{y}} &= \boldsymbol{\beta}_K + \boldsymbol{\Omega}_K \mathbf{h}_K \\ \end{aligned} \]

where \(\mathbf{a}(\cdot)\) is the element-wise activation function.

The square loss function is

\[ L = \sum_{i=1}^N \ell_i = \sum_{i=1}^N \|\mathbf{y}_i - \mathbf{\hat{y}}_i\|_2^2. \]

The total loss is the sum of the losses over the \(i\) training examples.

What we want to do is find weights in the NN that minimize the above loss function. We do this by

finding the partial derivatives of \(L\) with respect to each parameter in the network
updating the parameters with the negative of its partial derivatives

In other words, we compute

\[ \frac{\partial L}{\partial \boldsymbol{\beta}_k}, \frac{\partial L}{\partial \boldsymbol{\Omega}_k}, \frac{\partial L}{\partial \boldsymbol{\beta}_{k-1}}, \frac{\partial L}{\partial \boldsymbol{\Omega}_{k-1}}, \ldots, \frac{\partial L}{\partial \boldsymbol{\beta}_0}, \frac{\partial L}{\partial \boldsymbol{\Omega}_0}. \]

In the notation above, \(\boldsymbol{\beta}_k\) and \(\mathbf{\Omega}_k\) are the bias vectors and weight matrices of the \(k\)-th layer.

Just as with partial derivatives with respect to scalars, there are well-defined rules for how to compute the partial derivatives of vector and matrix expressions. PyTorch and TensorFlow implement these calculations.

The update rules for the parameters are given by

\[ \boldsymbol{\beta}_k \leftarrow \boldsymbol{\beta}_k - \eta\frac{\partial L}{\partial \boldsymbol{\beta}_k}, \]

\[ \boldsymbol{\Omega}_k \leftarrow \boldsymbol{\Omega}_k - \eta\frac{\partial L}{\partial \boldsymbol{\Omega}_k}, \]

where \(\eta\) is the learning rate.

Computation Graph

The way we are going to differentiate more complex functions is to first build a “computation graph.”

We’ll see that we can “propagate backwards” through the graph to calculate the gradients of the loss function with respect to the parameters.

It’s a scalable approach employed by TensorFlow and PyTorch, and in fact we’ll follow PyTorch interface definition.

Building the `Value` Class

To do that we will

build a data wrapper as a class called Value,
gradually build in on all the functionality we need to define a Multi-Layer Neural Network (a.k.a. Multi-Layer Perceptron),
and train the full network.

This is similar to how PyTorch defines its Tensor class.

First, the class has only a simple initialization method and a representation method.

# Value version 1
class Value:

    def __init__(self, data):
        self.data = data

    def __repr__(self):
        """Return a string representation of the object for display"""
        return f"Value(data={self.data})"

Which we can instantiate and evaluate as follows.

a = Value(4.0)
a

Value(data=4.0)

If you are not familiar with python classes, there are a few things to note here.

The property self is just a pointer to the object itself.
The __init__ method is called when you initialize a class object.
The __repr__ method is how you represent the class object.

Implementing Addition

The Value object doesn’t do much yet except for taking a value and printing it. We’d also like to do things like addition and other operations with them, but…

a = Value(4.0)
b = Value(-3.0)

try:
    a+b 
except Exception as e:
    print("Uh oh!", e)
else:
    print("It worked!")

Uh oh! unsupported operand type(s) for +: 'Value' and 'Value'

When python tries to add two objects a and b, internally it will call a.__add__(b). We have to add the __add__() method.

# Value version 2
class Value:

    def __init__(self, data):
        self.data = data

    def __repr__(self):
        """Return a string representation of the object for display"""
        return f"Value(data={self.data})"

    def __add__(self, other):
        other = other if isinstance(other, Value) else Value(other)
        out = Value(self.data + other.data)
        return out

Now we try adding two Value objects again.

a = Value(4.0)
b = Value(-3.0)

try:
    a+b
except Exception as e:
    print("Uh oh!", e)
else:
    print("It worked!")

It worked!

Which, as mentioned is equivalent to calling the __add__ method on a.

a.__add__(b)

Value(data=1.0)

Implementing More Operations

Similarly we can add define a multiplication operation and a ReLU function.

import numpy as np

# Value version 3
class Value:

    def __init__(self, data):
        self.data = data

    def __repr__(self):
        """Return a string representation of the object for display"""
        return f"Value(data={self.data})"

    def __add__(self, other): # self + other
        other = other if isinstance(other, Value) else Value(other)
        out = Value(self.data + other.data)
        return out
    
    def __mul__(self, other): # self * other
        other = other if isinstance(other, Value) else Value(other)
        out = Value(self.data * other.data)
        return out
    
    def relu(self):
        out = Value(np.maximum(0, self.data))
        return out

Now we can use the additional operations.

a = Value(4.0)
b = Value(-3.0)
c = Value(8.0)

d = a*b+c
d

Value(data=-4.0)

d.relu()

Value(data=0.0)

Internally, python will call __mul__ on a, then __add__ on the temporary product object.

(a.__mul__(b)).__add__(c)

Value(data=-4.0)

Child Nodes

In order to calculate the gradients, we will need to capture the computation graphs.

To do that, we’ll need to store pointers to the operands of each operation as a tuple of child nodes in the initializer.

# Value version 4
class Value:
                        #    vvvvvvvvvvvv
    def __init__(self, data, _children=()):
        self.data = data
        self._prev = set(_children)

    def __repr__(self):
        """Return a string representation of the object for display"""
        return f"Value(data={self.data})"

    def __add__(self, other):
        other = other if isinstance(other, Value) else Value(other)
        out = Value(self.data + other.data, (self, other)) # store tuple of children
        return out                        # ^^^^^^^^^^^^^
    
    def __mul__(self, other):
        other = other if isinstance(other, Value) else Value(other)
        out = Value(self.data * other.data, (self, other)) # store tuple of children
        return out                        # ^^^^^^^^^^^^^
    
    def relu(self):
        out = Value(np.maximum(0, self.data), (self,))
        return out                         #  ^^^^^^^

Let’s instantiate a few Value objects and perform some operations with them.

a = Value(4.0)
b = Value(-3.0)
c = Value(8.0)

d = a*b
e = d + c

We can now see the children of the operands that produced the output value by printing the _prev value. The name _prev might not be intuitive yet, but it will make more sense when we view these operations as a graph.

d._prev

{Value(data=-3.0), Value(data=4.0)}

e._prev

{Value(data=-12.0), Value(data=8.0)}

Child Operations

Now we’ve recorded pointers to the child nodes. It would be helpful to also record the operator used.

We’ll also add labels for convenience.

# Value version 5
class Value:
                                    #     vvvvvvv  vvvvvvvv
    def __init__(self, data, _children=(), _op='', label=''):
        self.data = data
        self._prev = set(_children)
        self._op = _op # store the operation that created this node
        self.label = label # label for the node

    def __repr__(self):
        """Return a string representation of the object for display"""
        return f"Value(data={self.data})"

    def __add__(self, other):
        other = other if isinstance(other, Value) else Value(other)   
        out = Value(self.data + other.data, (self, other), '+') # store operator used
        return out                                      #  ^^^
    
    def __mul__(self, other):
        other = other if isinstance(other, Value) else Value(other)
        out = Value(self.data * other.data, (self, other), '*') # store operator used
        return out                                      #  ^^^
    
    def relu(self):                                 #  vvvvvv
        out = Value(np.maximum(0, self.data), (self,), 'ReLU')

        return out

Let’s again instantiate a few Value objects and do some operations with them.

a = Value(4.0, label='a')
b = Value(-3.0, label='b')
c = Value(8.0, label='c')

d = a*b ; d.label = 'd'
e = d + c ; e.label = 'e'

We can now inspect the parent operands and the operations used to create the current node value.

d._prev, d._op, d.label

({Value(data=-3.0), Value(data=4.0)}, '*', 'd')

e._prev, e._op, e.label

({Value(data=-12.0), Value(data=8.0)}, '+', 'e')

The Compute Graph

We now have enough information stored about the compute graph to visualize it.

These are two functions to walk the graph and build sets of all nodes and edges (trace) and then draw them as a directed graph (draw_dot).

Show the code for trace() and draw_dot()

# draw_dot version 1
from graphviz import Digraph

def trace(root):
  # builds a set of all nodes and set of all edges in a graph
  nodes, edges = set(), set()
  def build(v):
    if v not in nodes:
      nodes.add(v)
      for child in v._prev:
        edges.add((child, v))
        build(child)
  build(root)
  return nodes, edges

def draw_dot(root):
  dot = Digraph(format='svg', graph_attr={'rankdir': 'LR'}) # LR = left to right

  nodes, edges = trace(root)
  for n in nodes:
    uid = str(id(n))
    # for any value in the graph, create a rectangular ('record') node for it
    dot.node(name = uid, label = "{ %s | data %.4f }" % (n.label, n.data), shape='record')
    if n._op:
      # if this value is a result of some operation, create an op node for it
      dot.node(name = uid + n._op, label = n._op)
      # and connect this no de to it
      dot.edge(uid + n._op, uid)

  for n1, n2 in edges:
    # connect n1 to the op node of n2
    dot.edge(str(id(n1)), str(id(n2)) + n2._op)

  return dot

a = Value(4.0, label='a')
b = Value(-3.0, label='b')
c = Value(8.0, label='c')

d = a*b ; d.label = 'd'
e = d + c ; e.label = 'e'

draw_dot(e)

Note that every value object becomes a node in the graph. The operators are also represented as a kind of fake node so they can be visualized too.

nodes, edges = trace(e)
print("Nodes: ", nodes)
print("Edges: ", edges)

Nodes:  {Value(data=-12.0), Value(data=-3.0), Value(data=4.0), Value(data=8.0), Value(data=-4.0)}
Edges:  {(Value(data=8.0), Value(data=-4.0)), (Value(data=4.0), Value(data=-12.0)), (Value(data=-3.0), Value(data=-12.0)), (Value(data=-12.0), Value(data=-4.0))}

Lets add one more operation, or stage, in the compute graph.

a = Value(4.0, label='a')
b = Value(-3.0, label='b')
c = Value(8.0, label='c')

d = a*b; d.label = 'd'
e = d + c; e.label = 'e'
f = Value(2.0, label='f')

L = e*f; L.label = 'L'

draw_dot(L)

Recap

So far we’ve:

built a Value class and associated data structures,
captured a computational graph, and
calculated the output based on the inputs and operations.

We’ll call this the forward pass (or forward propagation).

We now need to calculate the gradient of the loss function \(L\) with respect to the parameters of the model.

Next we’ll update our Value class to capture the partial derivative at each node relative to L.

Calculating Gradients

We now add a gradient member variable, grad, to our class to store the partial derivative of the node with respect to the output node.

# Value version 6
class Value:

    def __init__(self, data, _children=(), _op='', label=''):
        self.data = data
        self.grad = 0.0 # default to 0  <<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
        self._prev = set(_children)
        self._op = _op # store the operation that created this node
        self.label = label # label for the node

    def __repr__(self):
        """Return a string representation of the object for display"""
        return f"Value(data={self.data})"

    def __add__(self, other):
        other = other if isinstance(other, Value) else Value(other)   
        out = Value(self.data + other.data, (self, other), '+')
        return out
    
    def __mul__(self, other):
        other = other if isinstance(other, Value) else Value(other)   
        out = Value(self.data * other.data, (self, other), '*')
        return out
    
    def relu(self):         
        out = Value(np.maximum(0, self.data), (self,), 'ReLU')

        return out

We update draw_dot() to show grad in the node info.

Show the code for draw_dot()

# draw_dot version 2
from graphviz import Digraph

def trace(root):
  # builds a set of all nodes and set of all edges in a graph
  nodes, edges = set(), set()
  def build(v):
    if v not in nodes:
      nodes.add(v)
      for child in v._prev:
        edges.add((child, v))
        build(child)
  build(root)
  return nodes, edges

def draw_dot(root):
  dot = Digraph(format='svg', graph_attr={'rankdir': 'LR'}) # LR = left to right
 
  nodes, edges = trace(root)
  for n in nodes:
    uid = str(id(n))
    # for any value in the graph, create a rectangular ('record') node for it
    dot.node(name = uid, label = "{ %s | data %.4f | grad %.4f }" % (n.label, n.data, n.grad), shape='record')
    if n._op:
      # if this value is a result of some operation, create an op node for it
      dot.node(name = uid + n._op, label = n._op)
      # and connect this node to it
      dot.edge(uid + n._op, uid)

  for n1, n2 in edges:
    # connect n1 to the op node of n2
    dot.edge(str(id(n1)), str(id(n2)) + n2._op)

  return dot

We also reinitialize and redraw the computational graph.

Code

a = Value(4.0, label='a')
b = Value(-3.0, label='b')
c = Value(8.0, label='c')

d = a*b; d.label = 'd'
e = d + c; e.label = 'e'
f = Value(2.0, label='f')

L = e*f; L.label = 'L'

draw_dot(L)

We have placeholders for the gradients, but they are currently all zero.

Manual Gradient Calculation

Before we start implementing backpropagation, it is helpful to manually calculate some gradients to better understand the procedure.

For the node \(L\), we trivially calculate \(\frac{dL}{dL} = 1\).

We can easily see this from the limit ratio perspective,

\[ \frac{dL}{dL} = \lim_{h \rightarrow 0} \frac{ (L+h) - L }{h} = \frac{h}{h} = 1 \]

Let’s set the gradient of the last node L to 1.

L.grad = 1.0

If we go backwards a step in the graph, we see that \(L=e*f\), so we calculate

\[ \frac{\partial{L}}{\partial{e}} = \frac{\partial}{\partial{e}} (e\times f) = f, \]

and

\[ \frac{\partial{L}}{\partial{f}} = \frac{\partial}{\partial{f}} (e\times f) = e. \]

So we just assign the gradient value to the value of the other operand node.

e.grad = f.data
f.grad = e.data

Tip

For products, the partial derivative w.r.t. to one operand is simply the other operand.

Important

We needed the node values, e.g., e.data and f.data, in order to update the gradients. Remember, we calculate all the node values in the forward pass.

We again redraw the above computational graph .

draw_dot(L)

How do the parameters \(e\) and \(f\) influence \(L\)? Here’s a function to vary (or wiggle) them and see the effect on \(L\).

# Try uncommenting `e += h` or `f += h` and calling `wiggle()` then `wiggle(1.0)`
# to see the influence of e or f on L
def wiggle(h = 0.0):
    a = Value(4.0, label='a')
    b = Value(-3.0, label='b')
    c = Value(8.0, label='c')

    d = a*b; d.label = 'd'
    e = d + c; e.label = 'e'
    # e += h
    f = Value(2.0, label='f')
    f += h

    L = e*f; L.label = 'L'
    print(L)

Let’s invoke it with no change \(0\) and then a change of \(1\).

wiggle(0.0)

Value(data=-8.0)

wiggle(1.0)

Value(data=-12.0)

Question

What does \(L\) change by if we change \(f\) by 1?

How much would \(L\) change if we changed \(e\) by 1?

Comment line 12 and uncomment line 10 to check your answer.

Propagating Back

Code

draw_dot(L)

Now we want to calculate

\[ \frac{\partial{L}}{\partial{c}}, \]

i.e., we want to know how much \(L\) varies if we vary \(c\), or how \(c\) influences \(L\).

Looking at the graph again we see that \(c\) influences \(e\) and \(e\) influences \(L\), so we should be able see the ripple effect of \(c\) on \(L\).

\[ c \rightarrow e \rightarrow L. \]

We have that \(e = c + d\), and so we calculate

\[ \frac{\partial{e}}{\partial{c}} = \frac{\partial{}}{\partial{c}} (d + c) = 1. \]

Tip

For addition, the partial derivative w.r.t. to one operand is 1.

Question

\[ c \rightarrow e \rightarrow L \]

Now we know \(\partial{L}/\partial{e}\) and we also know \(\partial{e}/\partial{c}\),

How do we get \(\partial{L}/\partial{c}\)?

The Chain Rule

To paraphrase from the Wikipedia page on Chain rule, if a variable \(L\) depends on the variable \(e\), which itself depends on the variable \(c\), then \(L\) depends on \(c\) as well, via the intermediate variable \(e\).

In this case, the chain rule is expressed as

\[ \frac{\partial L}{\partial c} = \frac{\partial L}{\partial e} \cdot \frac{\partial e}{\partial c}, \]

and

\[ \left.\frac{\partial L}{\partial c}\right|_{c} = \left.\frac{\partial L}{\partial e}\right|_{e(c)}\cdot \left. \frac{\partial e}{\partial c}\right|_{c}. \]

The above notation indicates at which points the derivatives have to be evaluated.

We evaluate the derivatives at the specific values of the variables that we calculated in the forward pass.

Since we’ve established that

\[ \frac{\partial{e}}{\partial{c}} = 1, \]

then

\[ \frac{\partial L}{\partial c} = \frac{\partial L}{\partial e} \cdot \frac{\partial{e}}{\partial{c}} = \frac{\partial L}{\partial e} \cdot 1. \]

In the case of an operand in an addition operation, we just copy the gradient of the parent node.

Or put another way:

Important

With the addition operator, we just route the parent gradient to the child.

So let’s assign the gradient of e to d and c.

d.grad = e.grad
c.grad = e.grad

And redraw the graph.

How does \(c\) and \(d\) influence \(L\)?

# Try uncommenting `c += h` or `d += h` and calling `wiggle()` then `wiggle(1.0)`
# to see the influence of c or d on L
def wiggle(h = 0.0):
    a = Value(4.0, label='a')
    b = Value(-3.0, label='b')
    c = Value(8.0, label='c')
    c += h

    d = a*b; d.label = 'd'
    # d += h

    e = d + c; e.label = 'e'
    f = Value(2.0, label='f')

    L = e*f; L.label = 'L'
    print(L)

Let’s look at the effect c has on L.

wiggle(0.0)

Value(data=-8.0)

wiggle(1.0)

Value(data=-6.0)

Change the code to see the effect of d on L.

Propagating Back Again

Now we want to calculate \(\frac{\partial{L}}{\partial{b}}\) and \(\frac{\partial{L}}{\partial{a}}\) but we have \(\frac{\partial{L}}{\partial{d}}\) and we know that

\[ \frac{\partial{d}}{\partial{b}} = \frac{\partial{}}{\partial{b}}(a\cdot b) = a, \]

so again from the chain rule

\[ \frac{\partial{L}}{\partial{b}} = \frac{\partial{L}}{\partial{d}} \cdot \frac{\partial{d}}{\partial{b}} = \frac{\partial{L}}{\partial{d}} \cdot a. \]

If we expanded all the partial derivatives, we would get

\[ \frac{\partial{L}}{\partial{b}} = \left(\frac{\partial{L}}{\partial{e}} \cdot \frac{\partial{e}}{\partial{d}}\right) \cdot \frac{\partial{d}}{\partial{b}}. \]

Let’s assign the gradient values to b and a.

b.grad = a.data * d.grad
a.grad = b.data * d.grad
draw_dot(L)

We’ve traversed all the way back to the inputs and calculated all the partial derivatives.

Now we can see the effects of varying b and a.

# Try uncommenting `a += h` or `b += h` and calling `wiggle()` then `wiggle(1.0)`
# to see the influence of a or b on L
def wiggle(h = 0.0):
    a = Value(4.0, label='a')
    # a += h
    b = Value(-3.0, label='b')
    b += h
    c = Value(8.0, label='c')

    d = a*b; d.label = 'd'

    e = d + c; e.label = 'e'
    f = Value(2.0, label='f')

    L = e*f; L.label = 'L'
    print(L)

Let’s look at the effect b has on L if we wiggle it by 0 and 1.

wiggle(0.0)

Value(data=-8.0)

wiggle(1.0)

Value(data=0.0)

Change the code to see the effect of a on L.

Recap

As you saw, we recursively went backwards through the computation graph and applied the local gradients to the gradients calculated so far to get the partial gradients.

We propagated this calculation backwards through the graph.

Of course, in practice, we will only need the gradients on the parameters, not the inputs, so we won’t bother calculating them on inputs.

Note

PyTorch let’s you control this by setting the requires_grad flag on Tensors.

This is the essence of Back Propagation.

Model Optimization

A Step in Optimization

Let’s take a look at the graph again.

draw_dot(L)

Assume we want the value of L to decrease.

We are free to change the values of the leaf nodes – all the other nodes are derived from children and leaf nodes.

The leaf nodes are \(a, b, c\) and \(f\).

In practice only update the parameter leaf nodes, not the input leaf node, but we’ll ignore that distinction temporarily for this example.

Let’s check the current value of L.

# remind ourselves what L is
print(L.data)

-8.0

As we showed before, we want to nudge each of those leaf nodes by the negative of the gradient, multiplied by a step size, \(\eta\), i.e.,

\[ w_{n+1} = w_n - \eta * \frac{\partial{L}}{\partial{w_n}}, \]

where \(n\) is the step number.

# nudge all the leaf nodes along the negative direction of the gradient
step_size = 0.01    # also called eta above

a.data -= step_size * a.grad
b.data -= step_size * b.grad
c.data -= step_size * c.grad
f.data -= step_size * f.grad

# recompute the forward pass
d = a*b
e = d + c
L = e*f

print(L.data)

-9.230591999999998

Observe that the value of L has indeed decreased.

A Single Neuron

Let’s programmatically define a single neuron with

two inputs
two weights (1 for each input)
a bias
the ReLU activation function

Recall the neuron figure above.

# inputs x1, x2
x1 = Value(2.0, label='x1')
x2 = Value(0.0, label='x2')

# weights w1, w2
w1 = Value(-3.0, label='w1')
w2 = Value(1.0, label='w2')

# bias of the neuron
b = Value(6.8813735870195432, label='b')

x1w1 = x1*w1; x1w1.label = 'x1*w1'
x2w2 = x2*w2; x2w2.label = 'x2*w2'

x1w1x2w2 = x1w1 + x2w2; x1w1x2w2.label = 'x1w1 + x2w2'
n = x1w1x2w2 + b; n.label = 'n'
o = n.relu(); o.label = 'o'

We can draw this compute graph:

draw_dot(o)

The only new operation we’ve added is the ReLU, so let’s take a quick look at how we differentiate the ReLU.

Like before, for the output node, o:

\[ \frac{\partial o}{\partial o} = 1. \]

o.grad = 1.0

ReLU is technically not differentiable at 0, but practically we implement the derivative as 0 when \(\le 0\) and 1 when \(1 > 0\)

n.grad = (o.data > 0) * o.grad  # = 0 when o.data <= 0; = o.grad when o.data > 0

Coding Backpropagation

We’ll update our Value class once more to support the backward pass.

There’s a

private _backward() function in each operator that implements the local step of the chain rule, and
a backward() function in the class that topologically sorts the graph and calls the operator _backward() function starting at the end of the graph and going backward.

# version 7
class Value:

    def __init__(self, data, _children=(), _op='', label=''):
        self.data = data
        self.grad = 0.0 # default to 0, no impact on the output
        self._backward = lambda: None  # by default backward doesn't do anything
        self._prev = set(_children)
        self._op = _op
        self.label = label

    def __repr__(self):
        """Return a string representation of the object for display"""
        return f"Value(data={self.data}, grad={self.grad})"

    def __add__(self, other):
        other = other if isinstance(other, Value) else Value(other)
        out = Value(self.data + other.data, (self, other), '+')

        def _backward():
            self.grad += out.grad
            other.grad += out.grad
        out._backward = _backward

        return out

    def __mul__(self, other):
        other = other if isinstance(other, Value) else Value(other)
        out = Value(self.data * other.data, (self, other), '*')

        def _backward():
            self.grad += other.data * out.grad
            other.grad += self.data * out.grad
        out._backward = _backward
        return out

    def relu(self):
        out = Value(np.maximum(0, self.data), (self,), 'ReLU')
        # out = Value(0 if self.data < 0 else self.data, (self,), 'ReLU')

        def _backward():
            self.grad += (out.data > 0) * out.grad
        out._backward = _backward

        return out

    def backward(self):

        # topological order all of the children in the graph
        topo = []
        visited = set()
        def build_topo(v):
            if v not in visited:
                visited.add(v)
                for child in v._prev:
                    build_topo(child)
                topo.append(v)
        build_topo(self)

        # go one variable at a time and apply the chain rule to get its gradient
        self.grad = 1
        for v in reversed(topo):
            v._backward()

We redefined the class so we have to reinitialize the objects and run the operations again.

This constitutes the forward pass.

# inputs x1, x2
x1 = Value(2.0, label='x1')
x2 = Value(0.0, label='x2')

# weights w1, w2
w1 = Value(-3.0, label='w1')
w2 = Value(1.0, label='w2')

# bias of the neuron
#b = Value(6.7, label='b')
b = Value(6.8813735870195432, label='b')

x1w1 = x1*w1; x1w1.label = 'x1*w1'
x2w2 = x2*w2; x2w2.label = 'x2*w2'

x1w1x2w2 = x1w1 + x2w2; x1w1x2w2.label = 'x1w1 + x2w2'
n = x1w1x2w2 + b; n.label = 'n'
o = n.relu(); o.label = 'o'

So we’ve filled the data values for all the nodes, but haven’t calculated the gradients.

draw_dot(o)

All we have to do is call the backward() method of the last node…

o.backward()

and voila! We have all the gradients.

draw_dot(o)

Accumulating the Gradients

You might have noticed that we are accumulating the gradients.

This is because we calculate the gradient for each sample in a batch and then sum them up to calculate the average gradient for the batch.

The risk now is that if you don’t zero the gradients for the next iteration, you will have incorrect gradients.

Warning

Always remember to zero the gradient after each iteration where you update the parameters!

Accumulating the Gradients – Special Cases

There are also special cases to handle such as when a Value object is on both sides of the operand like

a = Value(3.0, label='a')
b = a + a ; b.label = 'b'
b.backward()

a

Value(data=3.0, grad=2.0)

If we didn’t have the accumulation, then a.grad = 1 instead.

Or the other case where a node goes to different operations.

a = Value(-2.0, label='a')
b = Value(3.0, label='b')
d = a * b  ; d.label = 'd'
e = a + b   ; e.label = 'e'
  
draw_dot(f)

Note

We can verify that the gradients are correct analytically.

To find the partial derivative \(\frac{\partial f}{\partial a}\), we first need to define \(f\) in terms of \(a\) and \(b\).

Given \[ \begin{aligned} d &= a \times b, \\ e &= a + b, \\ f &= d \times e \end{aligned} \]

then \(f\) can be expanded as \[ \begin{aligned} f &= (a \times b) \times (a + b), \\ &= a^2 \times b + a \times b^2. \end{aligned} \]

Next, we find the partial derivative of \(f\) with respect to \(a\) \[ \frac{\partial f}{\partial a} = 2a \times b + b^2. \]

Finally, we plug in the given values \(a = -2.0\) and \(b = 3.0\) \[ \begin{aligned} \frac{\partial f}{\partial a} &= 2(-2.0) \times 3.0 + 3.0^2, \\ \frac{\partial f}{\partial a} &= -12.0 + 9.0 , \\ \frac{\partial f}{\partial a} &= -3.0. \end{aligned} \]

So the partial derivative \(\frac{\partial f}{\partial a}\) for the value \(a = -2.0\) is \(-3.0\).

Enhancements to `Value` Class

There are still some useful operations that Value doesn’t support, so to be more complete we have the final version of the Value class below.

We added:

__radd__ for when the Value object is the right operand of an add
__rmul__ for when the Value object is the right operand of a product
__pow__ to support the ** operator
plus some others you can see below

The Value Class with additional operators

# version 8
class Value:

    def __init__(self, data, _children=(), _op='', label=''):
        self.data = data
        self.grad = 0.0 # default to 0, no impact on the output
        self._backward = lambda: None  # by default backward doesn't do anything
        self._prev = set(_children)
        self._op = _op
        self.label = label

    def __add__(self, other):
        other = other if isinstance(other, Value) else Value(other)
        out = Value(self.data + other.data, (self, other), '+')

        def _backward():
            self.grad += out.grad
            other.grad += out.grad
        out._backward = _backward

        return out
    
    def __mul__(self, other):
        other = other if isinstance(other, Value) else Value(other)
        out = Value(self.data * other.data, (self, other), '*')

        def _backward():
            self.grad += other.data * out.grad
            other.grad += self.data * out.grad
        out._backward = _backward
        
        return out

    def __pow__(self, other):
        """Adding support for ** operator, which we'll need for the 
        squared loss function"""
        assert isinstance(other, (int, float)), "only supporting int/float powers for now"
        out = Value(self.data**other, (self,), f'**{other}')

        def _backward():
            self.grad += (other * self.data**(other-1)) * out.grad
        out._backward = _backward

        return out

    def relu(self):
        out = Value(np.maximum(0, self.data), (self,), 'ReLU')

        def _backward():
            self.grad += (out.data > 0) * out.grad
        out._backward = _backward

        return out

    def __neg__(self): # -self
        return self * -1

    def __radd__(self, other): # other + self
        return self + other

    def __sub__(self, other): # self - other
        return self + (-other)

    def __rsub__(self, other): # other - self
        return other + (-self)

    def __rmul__(self, other): # other * self
        return self * other

    def __truediv__(self, other): # self / other
        return self * other**-1

    def __rtruediv__(self, other): # other / self
        return other * self**-1
    
    def backward(self):

        # topological order all of the children in the graph
        topo = []
        visited = set()
        def build_topo(v):
            if v not in visited:
                visited.add(v)
                for child in v._prev:
                    build_topo(child)
                topo.append(v)
        build_topo(self)

        # go one variable at a time and apply the chain rule to get its gradient
        self.grad = 1
        for v in reversed(topo):
            v._backward()

    def __repr__(self):
        """Return a string representation of the object for display"""
        return f"Value(data={self.data}, grad={self.grad})"

Comparing to PyTorch

We’re using a class implementation that resembles the PyTorch implementation, and in fact we can compare our implementation with PyTorch.

import torch

x1 = torch.Tensor([2.0]).double()                ; x1.requires_grad = True
x2 = torch.Tensor([0.0]).double()                ; x2.requires_grad = True
w1 = torch.Tensor([-3.0]).double()               ; w1.requires_grad = True
w2 = torch.Tensor([1.0]).double()                ; w2.requires_grad = True
b = torch.Tensor([6.8813735870195432]).double()  ; b.requires_grad = True
n = x1*w1 + x2*w2 + b
o = torch.relu(n)

print(o.data.item())
o.backward()

print('---')
print('x2.grad', x2.grad.item())
print('w2.grad', w2.grad.item())
print('x1.grad', x1.grad.item())
print('w1.grad', w1.grad.item())

0.881373405456543
---
x2.grad 1.0
w2.grad 0.0
x1.grad -3.0
w1.grad 2.0

By default, tensors don’t store gradients and so won’t support backprop, so we explicitly set requires_grad = True.

Building a Neural Network

Neural Network Modules

Now we’ll define some classes which help us build out a small neural network.

Module – A base class

Neuron – Implement a single linear or nonlinear neuron with nin inputs.

Layer – Implement a layer of network consisting of nout neurons, each taking nin inputs

MLP – A Multi-Layer Perceptron that implements len(nouts) layers of neurons.

Each class can calculate a forward pass and enumerate all its parameters.

Code

import random
# we assume that Value class is already defined

class Module:
    """Define a Neural Network Module base class """

    def zero_grad(self):
        """When we run in a training loop, we'll need to zero out all the gradients
        since they are defined to accumulate in the backwards passes."""
        for p in self.parameters():
            p.grad = 0

    def parameters(self):
        return []

class Neuron(Module):
    """Define a Neuron as a subclass of Module"""

    def __init__(self, nin, nonlin=True):
        """Randomly initialize a set of weights, one for each input, and initialize the bias to zero."""
        self.w = [Value(random.uniform(-1,1)) for _ in range(nin)]
        self.b = Value(0.0)
        self.nonlin = nonlin

    def __call__(self, x):
        """Implement the forward pass of the neuron"""
        act = sum((wi*xi for wi,xi in zip(self.w, x)), self.b)
        return act.relu() if self.nonlin else act

    def parameters(self):
        return self.w + [self.b]

    def __repr__(self):
        return f"{'ReLU' if self.nonlin else 'Linear'}Neuron({len(self.w)})"

class Layer(Module):
    """Define a Layer of Network as a subclass of Module"""

    def __init__(self, nin, nout, **kwargs):
        """Initialize nout Neurons, each with nin inputs"""
        self.neurons = [Neuron(nin, **kwargs) for _ in range(nout)]

    def __call__(self, x):
        """Forward pass each neuron in the layer"""
        out = [n(x) for n in self.neurons]
        return out[0] if len(out) == 1 else out

    def parameters(self):
        return [p for n in self.neurons for p in n.parameters()]

    def __repr__(self):
        return f"Layer of [{', '.join(str(n) for n in self.neurons)}]"

class MLP(Module):
    """Define a Multi-Layer Perceptron"""

    def __init__(self, nin: int, nouts: list):
        """
        Initialize the Multi-Layer Perceptron, by initializing each layer
        then initializing each neuron of each layer.

        Parameters:
            nin: Number of inputs (int)
            nouts: A list of the number of neurons in each layer
        """
        sz = [nin] + nouts
        # self.layers = [Layer(sz[i], sz[i+1]) for i in range(len(nouts))]

        # Create a list of layer objects for this MLP. All but the last layer
        # have ReLU activations. The last layer is linear.
        self.layers = [Layer(sz[i], sz[i+1], nonlin=i!=len(nouts)-1) for i in range(len(nouts))]

    def __call__(self, x):
        """Forward pass through the MLP"""
        for layer in self.layers:
            x = layer(x)
        return x

    def parameters(self):
        """Recursively retrieve the parameters of the MLP"""
        return [p for layer in self.layers for p in layer.parameters()]

    def __repr__(self):
        return f"MLP of [{', '.join(str(layer) for layer in self.layers)}]"

Feel free to uncomment lines of code in the following cell to see the docstrings for each class.

# help(Module)
# Module.__doc__
# help(Neuron)
# help(Layer)
# help(MLP)

Initialize and Evaluate a Neuron

# 2 inputs
x = [2.0, 3.0]

# initialize neuron with 2 inputs
n = Neuron(2, nonlin=False)

# evaluate our neuron with our 2 inputs
n(x)

Value(data=-0.7986044827378151, grad=0.0)

LinearNeuron(2)

# list the 2 weights and the bias
n.parameters()

[Value(data=0.13662034202253892, grad=0.0),
 Value(data=-0.35728172226096433, grad=0.0),
 Value(data=0.0, grad=0.0)]

Initialize and Evaluate a Layer

# same 2 inputs again
x = [2.0, 3.0]

# Now initialize a layer of 3 neurons, each with 2 inputs
l = Layer(2, 3, nonlin=False)

# Evaluate our layer of neurons with the 2 inputs
l(x)

[Value(data=2.075707642189308, grad=0.0),
 Value(data=3.317750385687485, grad=0.0),
 Value(data=1.3166915978118992, grad=0.0)]

Layer of [LinearNeuron(2), LinearNeuron(2), LinearNeuron(2)]

l.parameters()

[Value(data=-0.15375774313175783, grad=0.0),
 Value(data=0.7944077094842745, grad=0.0),
 Value(data=0.0, grad=0.0),
 Value(data=0.7480309600826056, grad=0.0),
 Value(data=0.6072294885074245, grad=0.0),
 Value(data=0.0, grad=0.0),
 Value(data=-0.5977201965507355, grad=0.0),
 Value(data=0.8373773303044567, grad=0.0),
 Value(data=0.0, grad=0.0)]

Initialize and Evaluate an MLP

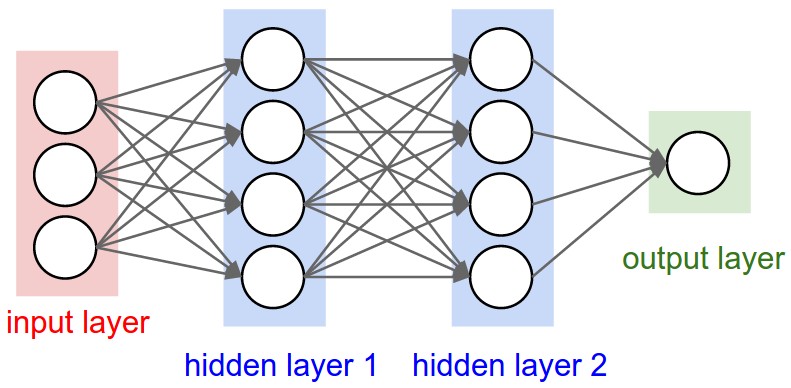
We’ll instantiate an MLP like the picture below.

x = [2.0, 3.0, -1.0]
m = MLP(3, [4, 4, 1])
m(x)

Value(data=3.882975961981558, grad=0.0)

MLP of [Layer of [ReLUNeuron(3), ReLUNeuron(3), ReLUNeuron(3), ReLUNeuron(3)], Layer of [ReLUNeuron(4), ReLUNeuron(4), ReLUNeuron(4), ReLUNeuron(4)], Layer of [LinearNeuron(4)]]

# m.parameters()

draw_dot(m(x))

Training Loop

In order to run the training loop, let’s define inputs, targets, and initialize the MLP.

# Define 4 different sets of inputs
xs = [
    [2.0, 3.0, -1.0],
    [3.0, -1.0, 0.5],
    [0.5, 1.0, 1.0],
    [1.0, 1.0, -1.0]
]

# For each input set, we have a desired target value -- binary classification
# ys = [1.0, -1.0, -1.0, 1.0]
ys = [1.0, 0.0, 0.0, 1.0]

# Manually seed the Random Number Generator for Reproducibility
# You can comment the next line out see the variability
random.seed(1) 

# Initialize an MLP with random weights
m = MLP(3, [4, 4, 1])

Now we can run the training loop.

losses = []
niters = 100
step_size = 0.01

for k in range(niters):

    # Training Step 1: forward pass
    ypred = [m(x) for x in xs]
    
    # Training Step 2: Calculate the loss
    loss = sum((yout - ygt)**2 for ygt, yout in zip(ys, ypred))
    losses.append(loss.data)

    # Training Step 3: Zero the gradients and run the backward pass
    m.zero_grad()
    loss.backward()

    # Training Step 4: Update parameters
    for p in m.parameters():
        p.data += -step_size * p.grad

    # print(k, loss.data)

print("Final Loss: ", loss.data)

Final Loss:  0.0073864224020347095

Let’s plot the loss per iteration.

plt.plot(losses)
plt.ylabel("Loss")
plt.xlabel("Iterations")
plt.title("Loss Per Iteration")

Text(0.5, 1.0, 'Loss Per Iteration')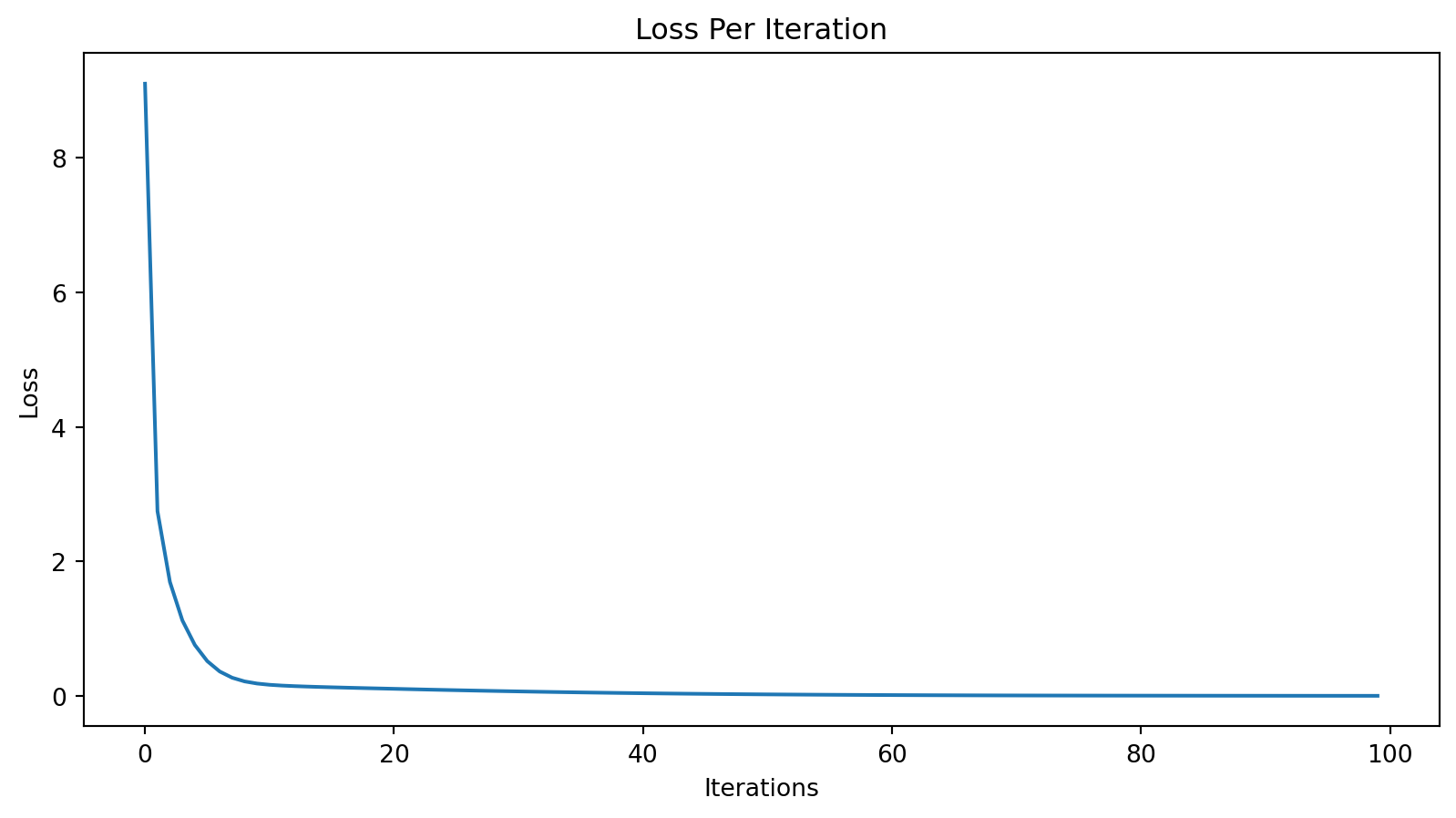

Let’s look at the ground truth and predictions.

print(type(ypred))
print(ypred[0].data)

list(zip(ys, [y.data for y in ypred]))

<class 'list'>
1.0120099058492713

[(1.0, np.float64(1.0120099058492713)),
 (0.0, np.float64(0.07244688900469765)),
 (0.0, np.float64(-0.03539087511088844)),
 (1.0, np.float64(0.9727765028706291))]

Build and Train the MLP in PyTorch

Define the MLP in PyTorch.

import torch
from torch import nn
from torch.optim import SGD

# Manually seed the Random Number Generator for Reproducibility
# You can comment the next line out see the variability
torch.manual_seed(99)

# Step 1: Define the MLP model
class ptMLP(nn.Module):
    def __init__(self):
        super(ptMLP, self).__init__()
        self.layers = nn.Sequential(
            nn.Linear(3, 4),
            nn.ReLU(),
            nn.Linear(4, 4),
            nn.ReLU(),
            nn.Linear(4, 1)
        )

    def forward(self, x):
        return self.layers(x)

model = ptMLP()
print(model)

ptMLP(
  (layers): Sequential(
    (0): Linear(in_features=3, out_features=4, bias=True)
    (1): ReLU()
    (2): Linear(in_features=4, out_features=4, bias=True)
    (3): ReLU()
    (4): Linear(in_features=4, out_features=1, bias=True)
  )
)

Define a loss function and an optimizer.

# Step 2: Define a loss function and an optimizer
criterion = nn.MSELoss(reduction='sum')
optimizer = SGD(model.parameters(), lr=0.01)

Recreate the tiny dataset.

# Step 3: Create a tiny dataset
xs = [
    [2.0, 3.0, -1.0],
    [3.0, -1.0, 0.5],
    [0.5, 1.0, 1.0],
    [1.0, 1.0, -1.0]
]

# we had to transpose ys for torch.tensor
ys_transpose = [[1.0], 
      [0.0], 
      [0.0], 
      [1.0]]

inputs = torch.tensor(xs)
outputs = torch.tensor(ys_transpose)

Now run the training loop.

# Step 4: Write the training loop
losses = []
niters = 100

for epoch in range(niters):

    # Training Step 1: Forward pass
    predictions = model(inputs)

    # Training Step 2: Calculate the loss
    loss = criterion(predictions, outputs)

    # Training Step 3: Zero the gradient and run backward pass
    optimizer.zero_grad()
    loss.backward()

    # Training Step 4: Update parameters
    optimizer.step()

    losses.append(loss.item())
    # print(f'Epoch {epoch+1}, Loss: {loss.item()}')

print(f'Final Loss: {loss.item()}')

Final Loss: 0.06534025073051453

Let’s plot the loss per iteration.

Code

plt.plot(losses)
plt.ylabel("Loss")
plt.xlabel("Iterations")
plt.title("Loss Per Iteration")

Text(0.5, 1.0, 'Loss Per Iteration')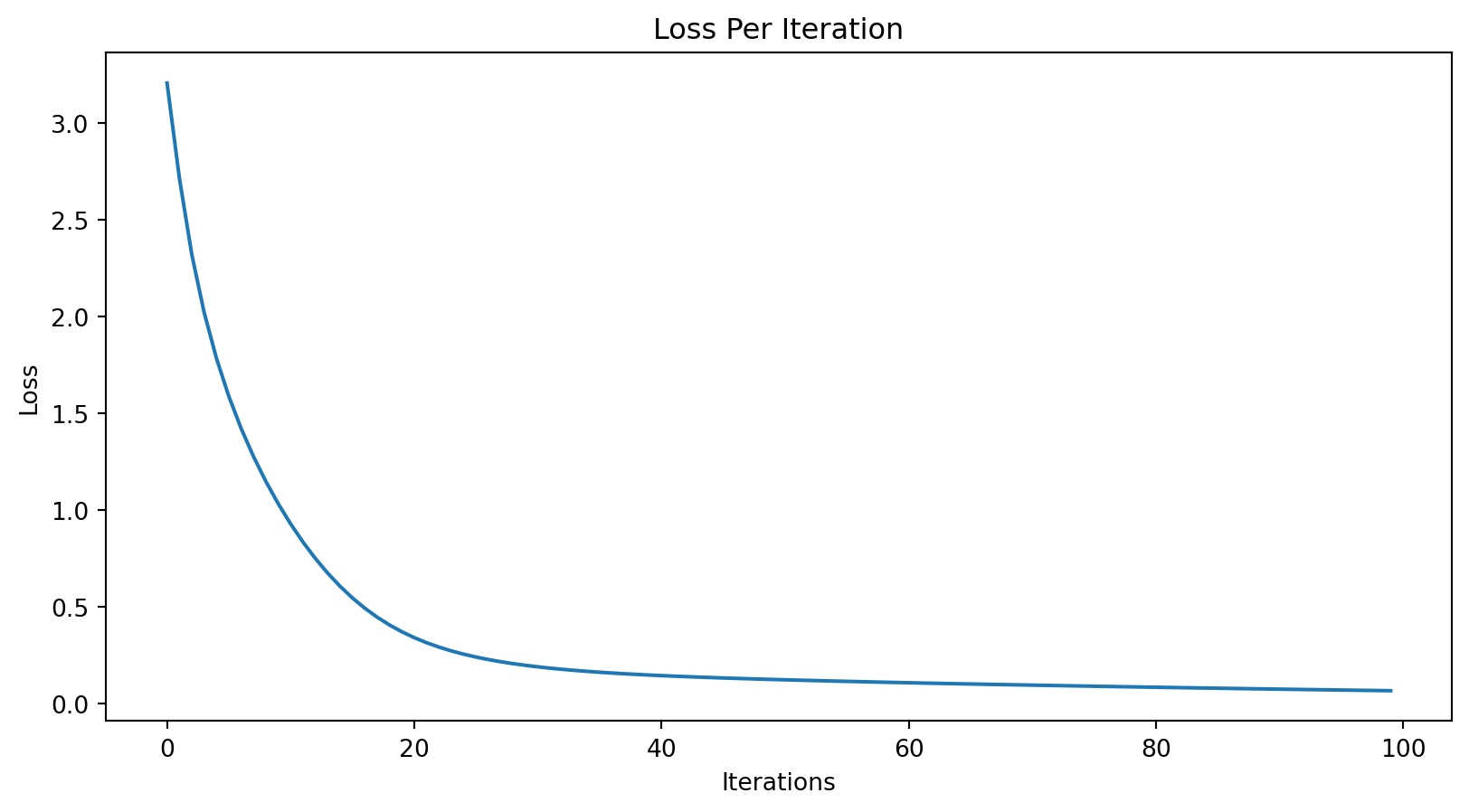

Let’s look at the predictions.

Code

list(zip(ys, [y.item() for y in predictions]))

[(1.0, 1.130600094795227),
 (0.0, 0.03639908879995346),
 (0.0, 0.017568498849868774),
 (1.0, 0.7840131521224976)]

To Dig a Little Deeper

PyTorch Quick Start Tutorial

TensorFlow Playground

Summary

We have now covered the following topics:

an overview of the wide applications of neural networks
loss functions
developed the notion of gradient descent first by intuition, then in the univariate case, then the multivariate case
defined artificial neurons
implemented a computation graph and visualization
implemented the chain rule as backpropagation on the computation graph
defined Neuron, Layer and MLP modules which completes a homegrown Neural Network Framework
trained a small MLP on a tiny dataset
implemented the same neural network architecture in PyTorch

Introduction

Artificial Neuron

Artificial Neuron

Activation Functions

Relating Back to an Earlier Lecture

Fully Connected Network (FCN)

Fully Connected Network (FCN)

FCN Matrix Equations

Computation Graph

Computation Graph

Building the Value Class

Implementing Addition

Implementing More Operations

Child Nodes

Child Operations

The Compute Graph

Recap

Calculating Gradients

Calculating Gradients

Manual Gradient Calculation

Propagating Back

Question

The Chain Rule

Propagating Back Again

Recap

Model Optimization

A Step in Optimization

A Single Neuron

Coding Backpropagation

Accumulating the Gradients

Accumulating the Gradients – Special Cases

Enhancements to Value Class

Comparing to PyTorch

Building a Neural Network

Neural Network Modules

Initialize and Evaluate a Neuron

Initialize and Evaluate a Layer

Initialize and Evaluate an MLP

Training Loop

Training Loop

Build and Train the MLP in PyTorch

To Dig a Little Deeper

Summary

Building the `Value` Class

Enhancements to `Value` Class