Linear Regression

Introduction

Introduction

Sir Francis Galton by Charles Wellington Furse

In 1886 Francis Galton published his observations about the height of children compared to their parents.

Regression to the Mean

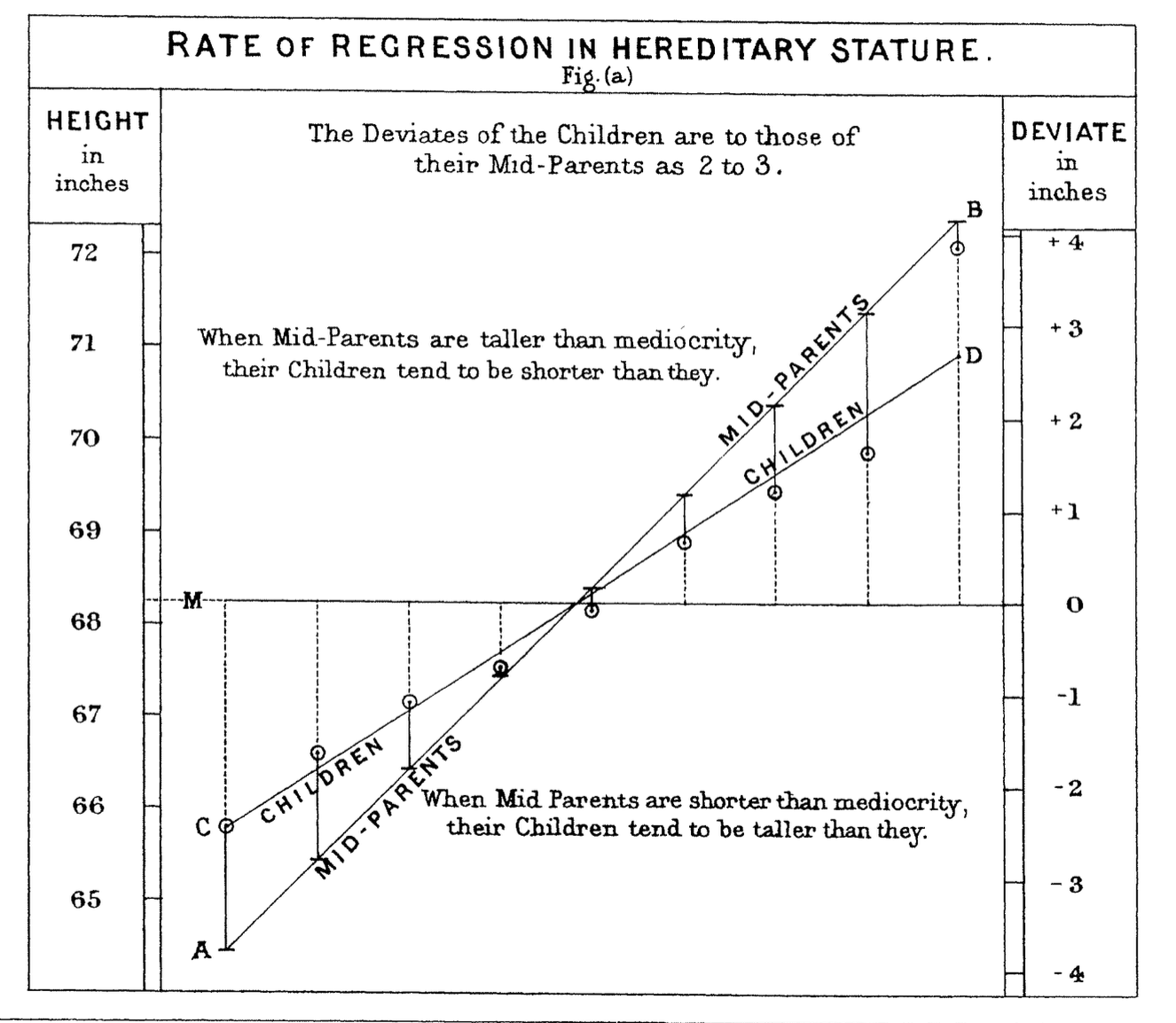
Defined mid-parent as the average of the heights of the parents.

When parents are taller or shorter than average, their children are more likely to be closer to the average height than their parents.

So called “regression to the mean.”

Galton fit a straight line to this effect, and the fitting of lines or curves to data has come to be called regression as well.

Praise versus Punishment

Daniel Kahneman

In the 60s, psychologist Daniel Kahneman studied the effect of praise versus punishment on performance of Israeli Air Force trainees. He was led to believe that praise was more effective than punishment.

Air force trainers disagreed and said that when they praised pilots that did well, they usually did worse the next time, and when they punished pilots that did poorly, they usually did better the next time.

What Khaneman later realised was that this phenomenon could be explained by the idea of regression to the mean.

If a pilot does worse than average on a task, they are more likely to do better the next time, and if they do better than average, they are more likely to do worse the next time.

Firing Coaches

NFL Coaches

Reference

Is it a good strategy to fire a coach after a bad season?

bad season -> fire and replace coach -> better season next year

When this could be interpreted as:

bad season (outlier) -> regression to the mean -> better season next year

This applies to many situations

“I had so many colds last year, and then I started herbal remedies, and I have much fewer colds this year.”

“My investments were doing quite bad last year, so switched investment managers, and now it is doing much better.”

When in fact, they could be (at least partially) explained by:

Regression to the mean

Model Types

The most common form of machine learning is regression, which means constructing an equation that describes the relationships among variables.

It is a form of supervised learning:

• whereas classification deals with predicting categorical features (labels or classes),
• regression deals with predicting continuous features (real values).

Fit to Linear Models

For example, we may look at these points and decide to model them using a line.

ax = plt.figure(figsize = (5, 5)).add_subplot()
centerAxes(ax)
line = np.array([1, 0.5])
xlin = -10.0 + 20.0 * np.random.random(100)
ylin = line[0] + (line[1] * xlin) + np.random.randn(100)
ax.plot(xlin, ylin, 'ro', markersize = 4)
plt.show()

Fit to Quadratic Models

We may look at these points and decide to model them using a quadratic function.

ax = plt.figure(figsize = (5, 5)).add_subplot()
centerAxes(ax)
quad = np.array([1, 3, 0.5])
std = 8.0
xquad = -10.0 + 20.0 * np.random.random(100)
yquad = quad[0] + (quad[1] * xquad) + (quad[2] * xquad * xquad) + std * np.random.randn(100)
ax.plot(xquad, yquad, 'ro', markersize = 4)
plt.show()

Fit to Logarithmic Models

And we may look at these points and decide to model them using a logarithmic function.

ax = plt.figure(figsize = (5, 5)).add_subplot()
centerAxes(ax)
log = np.array([1, 4])  
std = 1.5
xlog = 10.0 * np.random.random(100)
ylog = log[0] + log[1] * np.log(xlog) + std * np.random.randn(100)
ax.plot(xlog, ylog, 'ro', markersize=4)
plt.show()

Approach

Clearly, none of these datasets agrees perfectly with the proposed model.

So the question arises:

How do we find the best linear function (or quadratic function, or logarithmic function) given the data?

Framework

Framework

This problem has been studied extensively in the field of statistics.

Certain terminology is used:

• Some values are referred to as “independent,” and
• Some values are referred to as “dependent.”

The basic regression task is:

• given a set of independent variables
• and the associated dependent variables,
• estimate the parameters of a model (such as a line, parabola, etc) that describes how the dependent variables are related to the independent variables.

The independent variables are collected into a matrix \(X,\) sometimes called the design matrix.

The dependent variables are collected into an observation vector \(\mathbf{y}.\)

The parameters of the model (for any kind of model) are collected into a parameter vector \(\mathbf{\beta}.\)

ax = plt.figure(figsize = (5, 5)).add_subplot()
centerAxes(ax)
line = np.array([1, 0.5])
xlin = -10.0 + 20.0 * np.random.random(100)
ylin = line[0] + (line[1] * xlin) + np.random.randn(100)
ax.plot(xlin, ylin, 'ro', markersize = 4)
ax.plot(xlin, line[0] + line[1] * xlin, 'b-')
plt.text(-9, 3, r'$y = \beta_0 + \beta_1x$', size=20)
plt.show()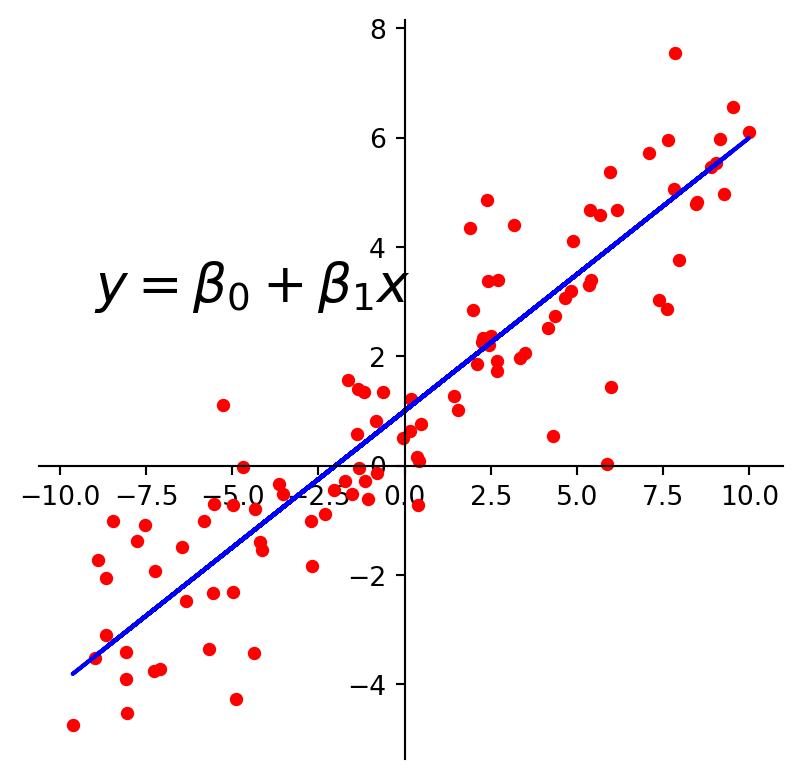

Least-Squares Lines

• The first kind of model we’ll study is a linear equation, \(y = \beta_0 + \beta_1 x.\)

• Experimental data often produce points \((x_1, y_1), \dots, (x_n, y_n)\) that seem to lie close to a line.

• We want to determine the parameters \(\beta_0, \beta_1\) that define a line that is as “close” to the points as possible.

Suppose we have a line \(y = \beta_0 + \beta_1 x\).

For each data point \((x_j, y_j),\) there is a point \((x_j, \beta_0 + \beta_1 x_j)\) that is the point on the line with the same \(x\)-coordinate.

import numpy as np
import matplotlib.pyplot as plt

# Generate some data points
x = np.array([1, 2, 3, 4, 5])
y = np.array([3.7, 2.0, 2.1, 0.1, 1.5])

# Linear regression parameters (intercept and slope)
beta_0 = 4  # intercept
beta_1 = -0.8  # slope

# Regression line (y = beta_0 + beta_1 * x)
y_line = beta_0 + beta_1 * x

# Create the plot
fig, ax = plt.subplots()
fig.set_size_inches(7, 4)

# Plot the data points
ax.scatter(x, y, color='blue', label='Data points', zorder=5)
ax.scatter(x, y_line, color='red', label='Predicted values', zorder=5)

# Plot the regression line
ax.plot(x, y_line, color='cyan', label='Regression line (y = β0 + β1x)', zorder=4)

# Add residuals (vertical lines from points to regression line)
for i in range(len(x)):
    ax.vlines(x[i], y_line[i], y[i], color='blue', linestyles='dashed', label='Residual' if i == 0 else "", zorder=2)

y_offset = [0.2, -0.2, 0.2, -0.2, 0.2]
y_line_offset = [-0.3, 0.3, -0.3, 0.3, -0.2]

# Annotate points
for i in range(len(x)):
    ax.text(x[i], y[i] + y_offset[i], f'({x[i]}, {y[i]})', fontsize=9, ha='center')
    ax.text(x[i], y_line[i] + y_line_offset[i], f'({x[i]}, {y_line[i]:.1f})', fontsize=9, ha='center')

# Remove the box around the plot and show only x and y axis with no tics and numbers
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
#ax.spines['left'].set_position('zero')
#ax.spines['bottom'].set_position('zero')
ax.xaxis.set_ticks([])
ax.yaxis.set_ticks([])

# Title
ax.set_title('Linear Regression with Residuals')

# Add legend
ax.legend()

# Show the plot
plt.show()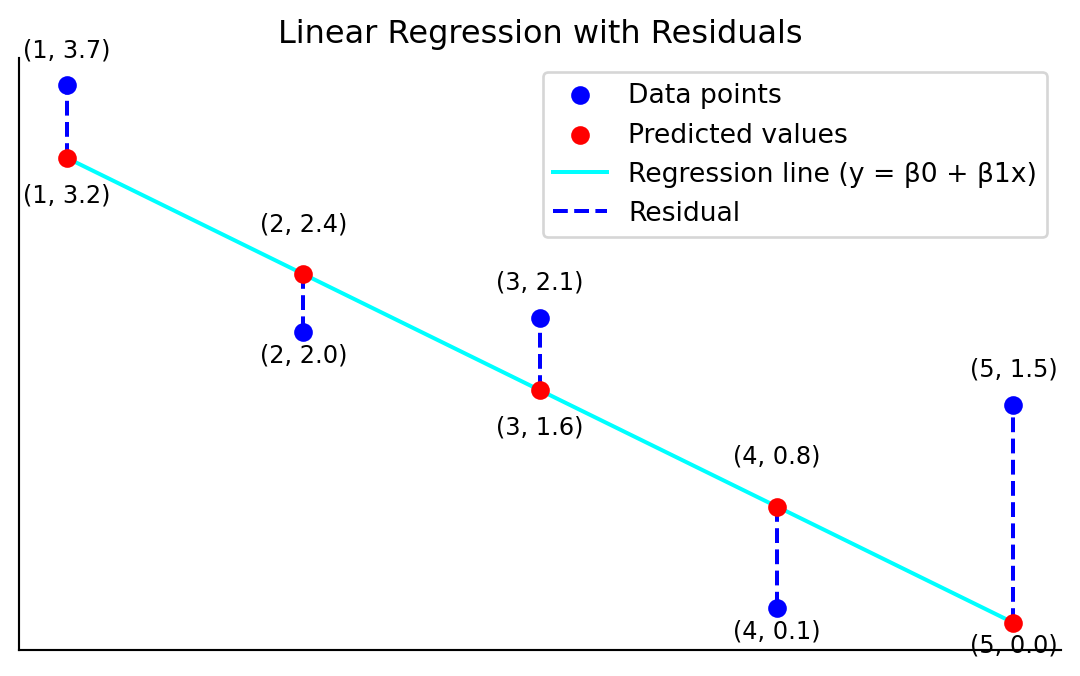

We call

• \(y_j\) the observed value of \(y\) and
• \(\beta_0 + \beta_1 x_j\) the predicted \(y\)-value.

The difference between an observed \(y\)-value and a predicted \(y\)-value is called a residual.

There are several ways to measure how “close” the line is to the data.

The usual choice is to sum the squares of the residuals.

The least-squares line is the line \(y = \beta_0 + \beta_1x\) that minimizes the sum of squares of the residuals.

The coefficients \(\beta_0, \beta_1\) of the line are called regression coefficients.

A least-squares problem

If the data points were on the line, the parameters \(\beta_0\) and \(\beta_1\) would satisfy the equations

\[ \begin{align*} \beta_0 + \beta_1 x_1 &= y_1, \\ \beta_0 + \beta_1 x_2 &= y_2, \\ \beta_0 + \beta_1 x_3 &= y_3, \\ &\vdots \\ \beta_0 + \beta_1 x_n &= y_n. \end{align*} \]

---

We can write this system as

\[ X\mathbf{\beta} = \mathbf{y}, \]

where

\[ X= \begin{bmatrix} 1 & x_1 \\ 1 & x_2 \\ \vdots & \vdots \\ 1 & x_n \end{bmatrix}, \;\;\mathbf{\beta} = \begin{bmatrix}\beta_0\\\beta_1\end{bmatrix}, \;\;\mathbf{y}=\begin{bmatrix}y_1\\y_2\\\vdots\\y_n\end{bmatrix}. \]

---

Of course, if the data points don’t actually lie exactly on a line,

… then there are no parameters \(\beta_0, \beta_1\) for which the predicted \(y\)-values in \(X\mathbf{\beta}\) equal the observed \(y\)-values in \(\mathbf{y}\),

… and \(X\mathbf{\beta}=\mathbf{y}\) has no solution.

---

Now, since the data doesn’t fall exactly on a line, we have decided to seek the \(\beta\) that minimizes the sum of squared residuals, i.e.,

\[ \sum_i (\beta_0 + \beta_1 x_i - y_i)^2 =\Vert X\beta -\mathbf{y}\Vert^2. \]

This is key:

Important

The sum of squares of the residuals is exactly the square of the distance between the vectors \(X\mathbf{\beta}\) and \(\mathbf{y}.\)

---

Computing the least-squares solution of \(X\beta = \mathbf{y}\) is equivalent to finding the \(\mathbf{\beta}\) that determines the least-squares line.

ax = plt.figure(figsize = (5, 5)).add_subplot()
centerAxes(ax)
line = np.array([1, 0.5])
xlin = -10.0 + 20.0 * np.random.random(100)
ylin = line[0] + (line[1] * xlin) + np.random.randn(100)
ax.plot(xlin, ylin, 'ro', markersize = 4)
ax.plot(xlin, line[0] + line[1] * xlin, 'b-')
plt.text(-9, 3, r'$y = \beta_0 + \beta_1x$', size=20)
plt.show()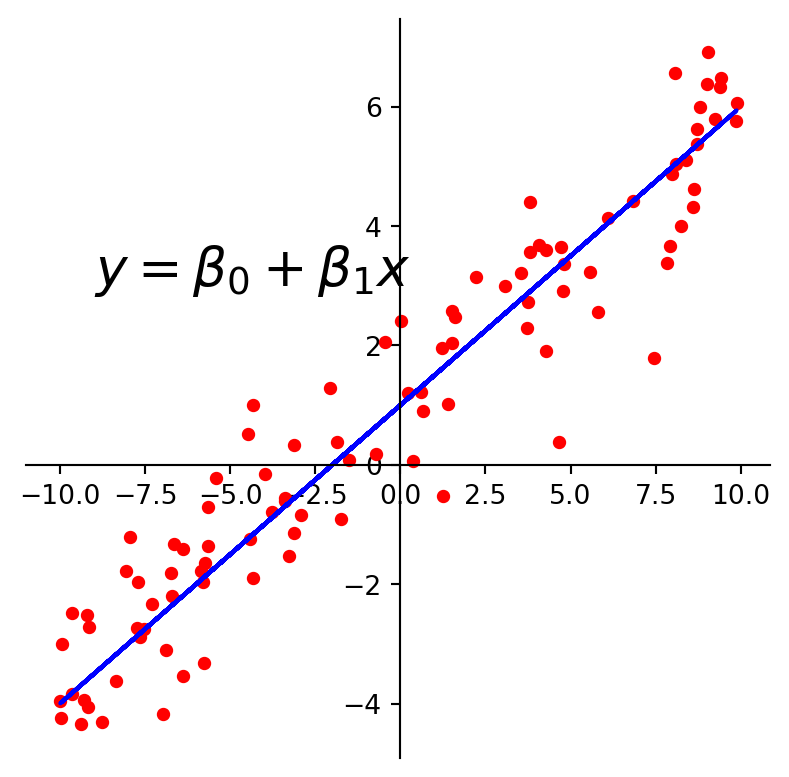

---

Now, to obtain the least-squares line, find the least-squares solution to \(X\mathbf{\beta} = \mathbf{y}.\)

From linear algebra we know that the least squares solution of \(X\mathbf{\beta} = \mathbf{y}\) is given by the solution of the normal equations:

\[ X^TX\mathbf{\beta} = X^T\mathbf{y}, \]

because \(X\mathbf{\beta} - \mathbf{y}\) is normal (e.g. orthogonal) to the column space of \(X.\)

We also know that the normal equations always have at least one solution.

And if \(X^TX\) is invertible, there is a unique solution that is given by:

\[ \hat{\mathbf{\beta}} = (X^TX)^{-1} X^T\mathbf{y}. \]

For \(X^T X\) to be invertible, where \(X\) is an \(n \times p\) matrix (n observations, p features):

1. \(X\) must have full column rank - i.e., \(\text{rank}(X) = p\)
2. We need \(n \geq p\) - at least as many observations as features
3. The columns of \(X\) must be linearly independent - no column can be written as a linear combination of the others

The General Linear Model

The General Linear Model

Another way that the inconsistent (.i.e. no exact solution) linear system is often written is to collect all the residuals into a residual vector.

Then an exact equation is

\[ y = X\mathbf{\beta} + {\mathbf\epsilon}, \]

where \(\mathbf{\epsilon}\) is the residual vector.

Any equation of this form is referred to as a linear model.

In this formulation, the goal is to find the \(\beta\) so as to minimize the norm of \(\epsilon\), i.e., \(\Vert\epsilon\Vert.\)

In some cases, one would like to fit data points with something other than a straight line.

In cases like this, the matrix equation is still \(X\mathbf{\beta} = \mathbf{y}\), but the specific form of \(X\) changes from one problem to the next.

Least-Squares Fitting of Other Models

In model fitting, the parameters of the model are what is unknown.

A central question for us is whether the model is linear in its parameters.

For example, is this model linear in its parameters?

\[ y = \beta_0 e^{-\beta_1 x} \]

It is not linear in its parameters.

Is this model linear in its parameters?

\[ y = \beta_0 e^{-2 x} \]

It is linear in its parameters.

---

For a model that is linear in its parameters, an observation is a linear combination of (arbitrary) known functions.

In other words, a model that is linear in its parameters is

\[ y = \beta_0f_0(x) + \beta_1f_1(x) + \dots + \beta_nf_n(x) \]

where \(f_0, \dots, f_n\) are known functions and \(\beta_0,\dots,\beta_n\) are parameters.

Example

Suppose data points \((x_1, y_1), \dots, (x_n, y_n)\) appear to lie along some sort of parabola instead of a straight line.

ax = plt.figure(figsize = (5, 5)).add_subplot()
centerAxes(ax)
quad = np.array([1, 3, 0.5])
xquad = -10.0 + 20.0 * np.random.random(100)
yquad = quad[0] + (quad[1] * xquad) + (quad[2] * xquad * xquad) + 2*np.random.randn(100)
ax.plot(xquad, yquad, 'ro', markersize = 4)
plt.show()

As a result, we wish to approximate the data by an equation of the form

\[ y = \beta_0 + \beta_1x + \beta_2x^2. \]

Let’s describe the linear model that produces a “least squares fit” of the data by the equation.

Solution

The ideal relationship is \(y = \beta_0 + \beta_1x + \beta_2x^2.\)

Suppose the actual values of the parameters are \(\beta_0, \beta_1, \beta_2.\)
Then the coordinates of the first data point satisfy the equation

\[ y_1 = \beta_0 + \beta_1x_1 + \beta_2x_1^2 + \epsilon_1, \]

where \(\epsilon_1\) is the residual error between the observed value \(y_1\) and the predicted \(y\)-value.

Each data point determines a similar equation:

\[ \begin{align*} y_1 &= \beta_0 + \beta_1x_1 + \beta_2x_1^2 + \epsilon_1, \\ y_2 &= \beta_0 + \beta_1x_2 + \beta_2x_2^2 + \epsilon_2, \\ &\vdots \\ y_n &= \beta_0 + \beta_1x_n + \beta_2x_n^2 + \epsilon_n. \end{align*} \]

---

Clearly, this system can be written as \(\mathbf{y} = X\mathbf{\beta} + \mathbf{\epsilon}.\)

\[ \begin{bmatrix} y_1\\ y_2\\ \vdots\\ y_n \end{bmatrix} = \begin{bmatrix}1&x_1&x_1^2\\ 1&x_2&x_2^2\\ \vdots&\vdots&\vdots\\ 1&x_n&x_n^2 \end{bmatrix} \begin{bmatrix} \beta_0\\\ \beta_1\\\ \beta_2 \end{bmatrix} + \begin{bmatrix} \epsilon_1\\ \epsilon_2\\ \vdots\\ \epsilon_n \end{bmatrix} \]

Let’s solve for \(\beta.\)

m = np.shape(xquad)[0]
X = np.array([np.ones(m), xquad, xquad**2]).T

# Solve for beta
beta = np.linalg.inv(X.T @ X) @ X.T @ yquad

And plot the results.

ax = ut.plotSetup(-10, 10, -10, 20)
ut.centerAxes(ax)
xplot = np.linspace(-10, 10, 50)
yestplot = beta[0] + beta[1] * xplot + beta[2] * xplot**2
ax.plot(xplot, yestplot, 'b-', lw=2)
ax.plot(xquad, yquad, 'ro', markersize=4)
plt.show()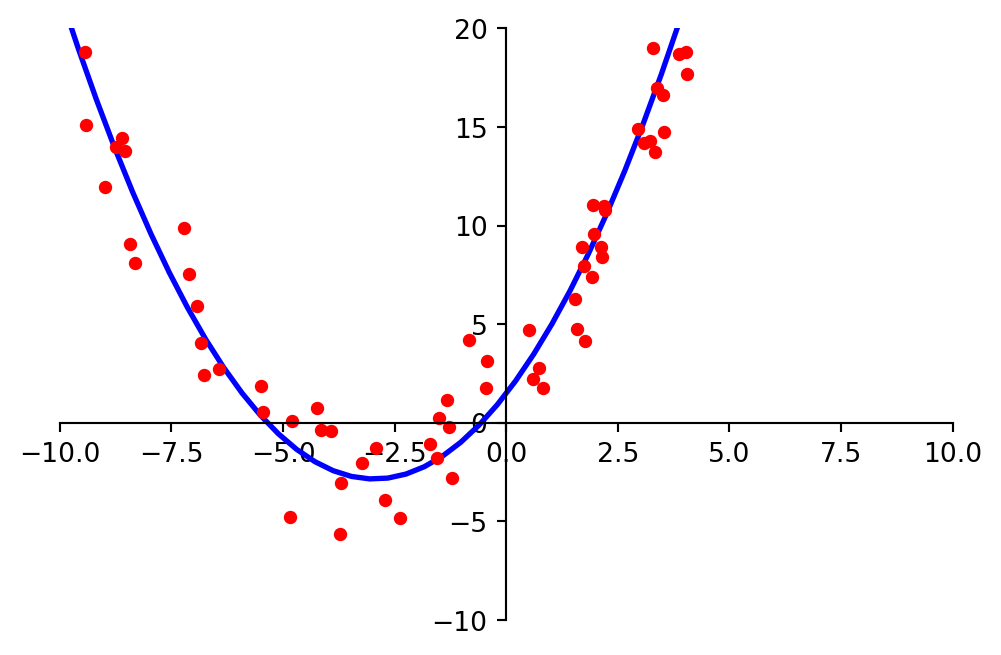

---

Now let’s try a different model.

\[ \begin{bmatrix} y_1\\ y_2\\ \vdots\\ y_n \end{bmatrix} = \begin{bmatrix}1&log(x_1)\\ 1&log(x_2)\\ \vdots&\vdots\\ 1&log(x_n) \end{bmatrix} \begin{bmatrix} \beta_0\\\ \beta_1 \end{bmatrix} + \begin{bmatrix} \epsilon_1\\ \epsilon_2\\ \vdots\\ \epsilon_n \end{bmatrix} \]

m = np.shape(xlog)[0]
X = np.array([np.ones(m), np.log(xlog)]).T

# Solve for beta
beta = np.linalg.inv(X.T @ X) @ X.T @ ylog

And plot the results.

# 
# plot the results
#
ax = ut.plotSetup(-10,10,-10,15)
ut.centerAxes(ax)
xplot = np.logspace(np.log10(0.0001),1,100)
yestplot = beta[0]+beta[1]*np.log(xplot)
ax.plot(xplot,yestplot,'b-',lw=2)
ax.plot(xlog,ylog,'ro',markersize=4)
plt.show()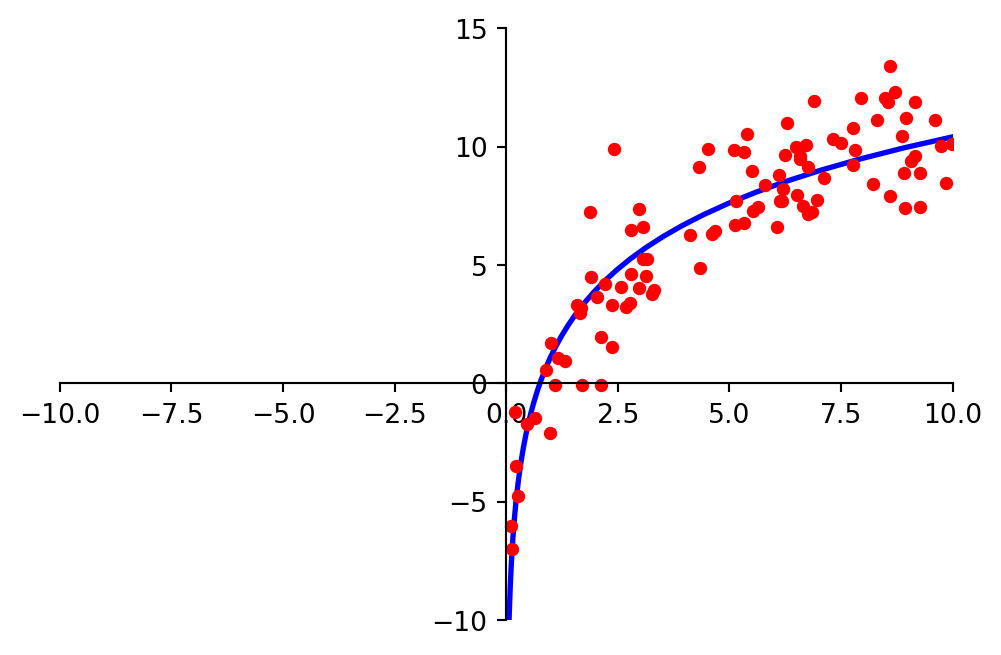

Multiple Regression

Suppose an experiment involves two independent variables – say, \(u\) and \(v\), – and one dependent variable, \(y\).

A simple equation for predicting \(y\) from \(u\) and \(v\) has the form

\[ y = \beta_0 + \beta_1 u + \beta_2 v. \]

Since there is more than one independent variable, this is called multiple regression.

A more general prediction equation might have the form

\[ y = \beta_0 + \beta_1 u + \beta_2 v + \beta_3u^2 + \beta_4 uv + \beta_5 v^2. \]

A least squares fit to equations like this is called a trend surface.

In general, a linear model will arise whenever \(y\) is to be predicted by an equation of the form

\[ y = \beta_0f_0(u,v) + \beta_1f_1(u,v) + \cdots + \beta_nf_n(u,v), \]

with \(f_0,\dots,f_n\) any sort of known functions and \(\beta_0,...,\beta_n\) unknown weights.

Example

Let’s take an example. Here are a set of points in \(\mathbb{R}^3\):

ax = ut.plotSetup3d(-7, 7, -7, 7, -10, 10, figsize = (5, 5))
v = [4.0, 4.0, 2.0]
u = [-4.0, 3.0, 1.0]
npts = 50

# set locations of points that fall within x,y
xc = -7.0 + 14.0 * np.random.random(npts)
yc = -7.0 + 14.0 * np.random.random(npts)
A = np.array([u,v]).T

# project these points onto the plane
P = A @ np.linalg.inv(A.T @ A) @ A.T
coords = P @ np.array([xc, yc, np.zeros(npts)])
coords[2] += np.random.randn(npts)
ax.plot(coords[0], coords[1], 'ro', zs=coords[2], markersize = 6)
plt.show()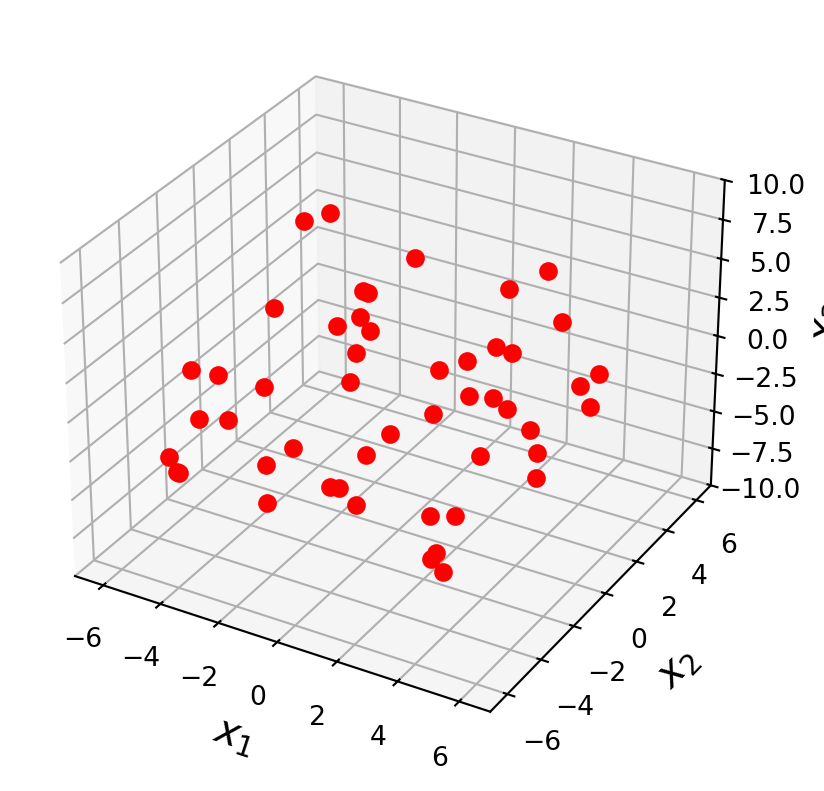

Example

In geography, local models of terrain are constructed from data

\[ (u_1, v_1, z_1), \dots, (u_n, v_n, z_n), \]

where \(u_j, v_j\), and \(z_j\) are latitude, longitude, and altitude, respectively.

Let’s describe the linear models that gives a least-squares fit to such data.
The solution is called the least-squares plane.

Solution

We expect the data to satisfy these equations:

\[ \begin{align*} y_1 &= \beta_0 + \beta_1 u_1 + \beta_2 v_1 + \beta_3 z_1 + \epsilon_1, \\ y_2 &= \beta_0 + \beta_1 u_2 + \beta_2 v_2 + \beta_3 z_2 + \epsilon_2, \\ \vdots \\ y_n &= \beta_0 + \beta_1 u_n + \beta_2 v_n + \beta_3 z_n + \epsilon_n. \end{align*} \]

This system has the matrix for \(\mathbf{y} = X\mathbf{\beta} + \epsilon,\) where

\[ \mathbf{y} = \begin{bmatrix}y_1\\ y_1\\ \vdots\\ y_n \end{bmatrix},\;\; X = \begin{bmatrix}1&u_1&v_1&z_1\\ 1&u_2&v_2&z_2\\ \vdots&\vdots&\vdots&\vdots\\ 1&u_n&v_n&z_n \end{bmatrix},\;\; \mathbf{\beta}= \begin{bmatrix} \beta_0\\ \beta_1\\ \beta_2\\ \beta_3 \end{bmatrix},\;\; \epsilon = \begin{bmatrix} \epsilon_1\\ \epsilon_2\\ \vdots\\ \epsilon_n \end{bmatrix}. \]

---

ax = ut.plotSetup3d(-7, 7, -7, 7, -10, 10, figsize = (7, 7))
v = [4.0, 4.0, 2.0]
u = [-4.0, 3.0, 1.0]

# plotting the span of v
ut.plotSpan3d(ax,u,v,'Green')
npts = 50
ax.plot(coords[0], coords[1], 'ro', zs = coords[2], markersize=6)
plt.show()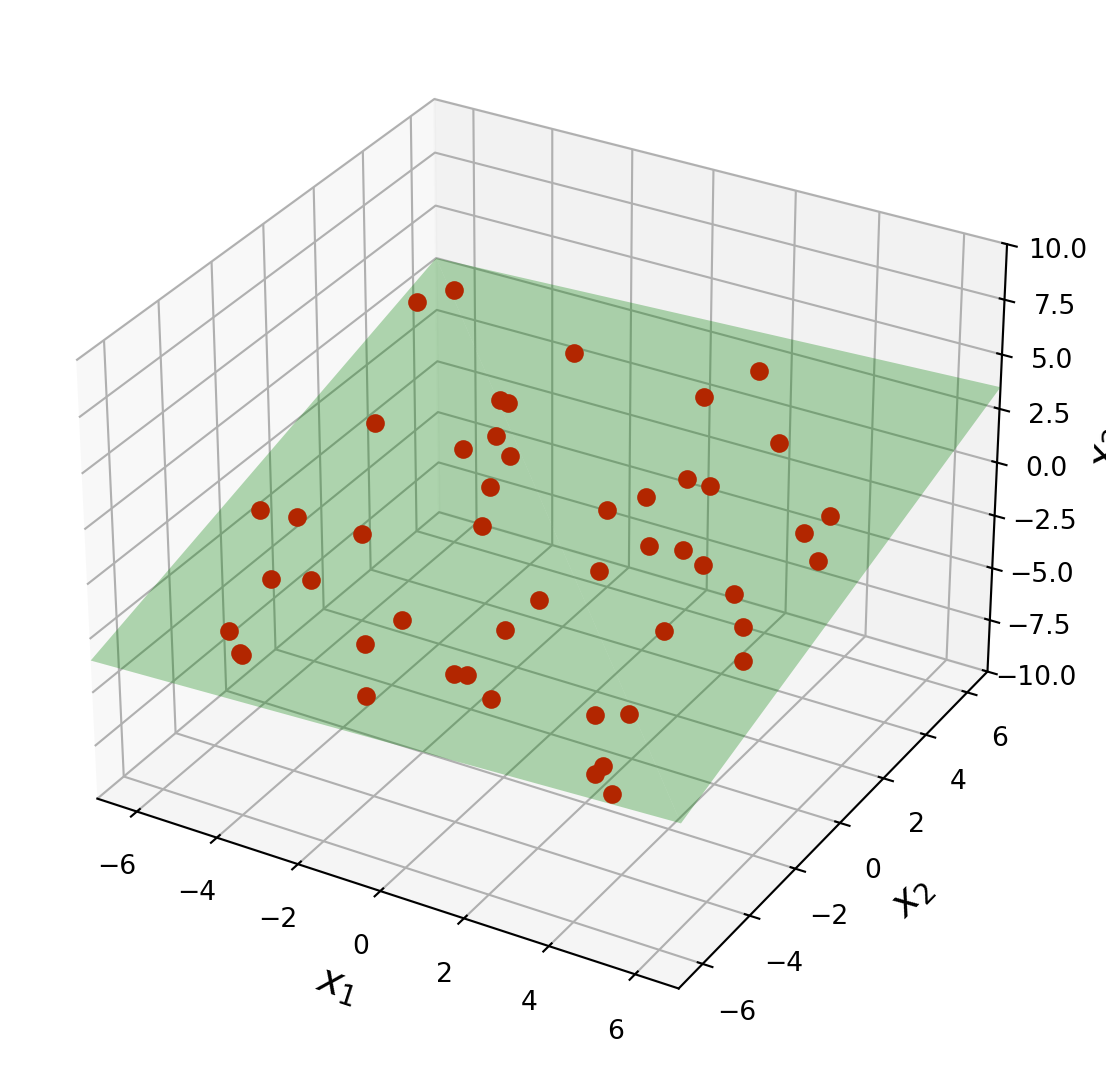

This example shows that the linear model for multiple regression has the same form as the model for the simple regression in the earlier examples.

We can see that the general principle is the same across all the different kinds of linear models.

Once \(X\) is defined properly, the normal equations for \(\mathbf{\beta}\) have the same matrix form, no matter how many variables are involved.

Thus, for any linear model where \(X^TX\) is invertible, the least squares estimate is

\[ \hat{\mathbf{\beta}} = (X^TX)^{-1}X^T\mathbf{y}. \]

Measuring the fit of a regression model: \(R^2\)

Given any \(X\) and \(\mathbf{y}\), the above algorithm will produce an output \(\hat{\beta}\).

But how do we know whether the data is in fact well described by the model?

The most common measure of fit is \(R^2\).

\(R^2\) measures the fraction of the variance of \(\mathbf{y}\) that can be explained by the model \(X\hat{\beta}\).

The variance of \(\mathbf{y}\) is

\[ \text{Var}(\mathbf{y}) =\frac{1}{n} \sum_{i=1}^n \left(y_i-\overline{y}\right)^2, \]

where \(\overline{y}=\frac{1}{n}\sum_{i=1}^ny_i\).

For any given \(n\), we can equally work with just \[ \sum_{i=1}^n \left(y_i-\overline{y}\right)^2, \]

which is called the Total Sum of Squares (TSS).

Total Sum of Squares

Now to measure the quality of fit of a model, we break TSS down into two components.

For any given \(\mathbf{x}_i\), the prediction made by the model is \(\hat{y_i} = \mathbf{x}_i^T\beta\).

We can break the total sum of squares into two parts:

• the residual \(\epsilon\) is \(y_i - \hat{y_i}\), and
• the part that the model “explains” is \(\hat{y_i} - \overline{y}.\)

RSS and ESS

Se we define the Residual Sum of Squares (RSS) as:

\[ \text{RSS} = \sum_{i=1}^n \left(y_i-\hat{y_i}\right)^2, \]

and the Explained Sum of Squares (ESS) as:

\[ \text{ESS} = \sum_{i=1}^n \left(\hat{y_i}-\overline{y}\right)^2, \]

One can show that the total sum of squares is exactly equal to the sum of squares of the residuals plus the sum of squares of the explained part.

In other words:

\[ \text{TSS} = \text{RSS} + \text{ESS}. \]

Proof that TSS = RSS + ESS

Given:

• TSS = \(\sum_{i=1}^n (y_i - \bar{y})^2\) (Total Sum of Squares)
• RSS = \(\sum_{i=1}^n (y_i - \hat{y}_i)^2\) (Residual Sum of Squares)
• ESS = \(\sum_{i=1}^n (\hat{y}_i - \bar{y})^2\) (Explained Sum of Squares)

Proof:

Start by decomposing the deviation from the mean: \[y_i - \bar{y} = (y_i - \hat{y}_i) + (\hat{y}_i - \bar{y})\]

Square both sides: \[\begin{align} (y_i - \bar{y})^2 &= [(y_i - \hat{y}_i) + (\hat{y}_i - \bar{y})]^2\\ &= (y_i - \hat{y}_i)^2 + 2(y_i - \hat{y}_i)(\hat{y}_i - \bar{y}) + (\hat{y}_i - \bar{y})^2 \end{align}\]

Sum over all \(i\): \[\sum_{i=1}^n (y_i - \bar{y})^2 = \sum_{i=1}^n (y_i - \hat{y}_i)^2 + 2\sum_{i=1}^n (y_i - \hat{y}_i)(\hat{y}_i - \bar{y}) + \sum_{i=1}^n (\hat{y}_i - \bar{y})^2\]

Which gives us: \[\text{TSS} = \text{RSS} + 2\sum_{i=1}^n (y_i - \hat{y}_i)(\hat{y}_i - \bar{y}) + \text{ESS}\]

The key step: We need to show that the cross-term equals zero: \[\sum_{i=1}^n (y_i - \hat{y}_i)(\hat{y}_i - \bar{y}) = 0\]

Why is this zero?

For OLS regression with an intercept, the residuals \((y_i - \hat{y}_i)\) satisfy two orthogonality conditions:

1. \(\sum_{i=1}^n (y_i - \hat{y}_i) = 0\) (residuals sum to zero)
2. \(\sum_{i=1}^n (y_i - \hat{y}_i)\hat{y}_i = 0\) (residuals are orthogonal to predictions)

Using condition (2): \[\sum_{i=1}^n (y_i - \hat{y}_i)(\hat{y}_i - \bar{y}) = \sum_{i=1}^n (y_i - \hat{y}_i)\hat{y}_i - \bar{y}\sum_{i=1}^n (y_i - \hat{y}_i) = 0 - \bar{y} \cdot 0 = 0\]

Therefore: TSS = RSS + ESS ✓

Geometric Intuition:

This decomposition is a Pythagorean theorem in high-dimensional space! The vectors \((y_i - \bar{y})\), \((y_i - \hat{y}_i)\), and \((\hat{y}_i - \bar{y})\) form a right triangle because the residuals are orthogonal to the fitted values.

Why residuals sum to exactly zero (with intercept)

Condition 1 is satisfied exactly (not just approximately), but this is only true when the model includes an intercept term.

When you include an intercept \(\beta_0\), the normal equations \(X^TX\beta = X^Ty\) include a row corresponding to the column of 1s in the design matrix.

Proof

Consider a linear model with an intercept. The design matrix has a column of 1s:

\[X = \begin{bmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1p} \\ 1 & x_{21} & x_{22} & \cdots & x_{2p} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & x_{n2} & \cdots & x_{np} \end{bmatrix}, \quad \beta = \begin{bmatrix} \beta_0 \\ \beta_1 \\ \vdots \\ \beta_p \end{bmatrix}, \quad y = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix}\]

The Normal Equations

The OLS solution satisfies the normal equations: \[X^T X \beta = X^T y\]

Looking at \(X^T\)

The transpose of \(X\) is: \[X^T = \begin{bmatrix} 1 & 1 & 1 & \cdots & 1 \\ x_{11} & x_{21} & x_{31} & \cdots & x_{n1} \\ x_{12} & x_{22} & x_{32} & \cdots & x_{n2} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_{1p} & x_{2p} & x_{3p} & \cdots & x_{np} \end{bmatrix}\]

The first row is all 1s!

The First Normal Equation

The normal equations give us a system of \((p+1)\) equations. The first equation comes from multiplying the first row of \(X^T\) with both sides:

Left side: First row of \(X^T\) times \(X\beta\) \[[1, 1, 1, \ldots, 1] \cdot X\beta = \sum_{i=1}^n (X\beta)_i = \sum_{i=1}^n \hat{y}_i\]

Right side: First row of \(X^T\) times \(y\) \[[1, 1, 1, \ldots, 1] \cdot y = \sum_{i=1}^n y_i\]

The Result

Therefore, the first normal equation is: \[\boxed{\sum_{i=1}^n \hat{y}_i = \sum_{i=1}^n y_i}\]

This is exact, not approximate. It’s a direct consequence of having the column of 1s in \(X\).

Interpretation

Dividing by \(n\): \[\bar{\hat{y}} = \bar{y}\]

The mean of the fitted values equals the mean of the observed values. This is why, with an intercept, the regression line always passes through the point \((\bar{x}, \bar{y})\).

End of proof

Without an intercept

If you force the regression through the origin (no \(\beta_0\) term), then:

• Condition 1 is NOT satisfied - residuals don’t sum to zero
• The TSS = RSS + ESS decomposition doesn’t hold
• \(R^2\) can even be negative!

The centered version assumes an intercept; the uncentered version doesn’t.

Key takeaway

For standard OLS with intercept: - \(\sum (y_i - \hat{y}_i) = 0\) ✓ (exactly) - \(\sum (y_i - \hat{y}_i)\hat{y}_i = 0\) ✓ (exactly, from normal equations)

Both are mathematical properties, not approximations!

\(R^2\), cont.

Now, a good fit is one in which the model explains a large part of the variance of \(\mathbf{y}\).

So the measure of fit \(R^2\) is defined as:

\[ R^2 = \frac{\text{ESS}}{\text{TSS}} = 1-\frac{\text{RSS}}{\text{TSS}} = 1 - \frac{\sum_{i=1}^n \left(y_i-\hat{y_i}\right)^2}{\sum_{i=1}^n \left(y_i-\overline{y}\right)^2}. \]

As a result, \(0\leq R^2\leq 1\).

This is more specifically called \(R^2\) centered.

There is also an uncentered version of \(R^2\) defined as:

\[ R^2 (\text{uncentered}) = 1 - \frac{\sum_{i=1}^n \left(y_i-\hat{y_i}\right)^2}{\sum_{i=1}^n y_i^2}. \]

The closer the value of \(R^2\) is to \(1\) the better the fit of the regression:

• small values of RSS imply that the residuals are small and therefore we have a better fit.

\(R^2\) is called the coefficient of determination.

It tells us “how well does the model predict the data?”

Warning

Do not confuse \(R^2\) with Pearson’s \(r\), which is the correlation coefficient.

(To make matters worse, sometimes people talk about \(r^2\)… very confusing!)

The correlation coefficient tells us whether two variables are correlated.

However, just because two variables are correlated does not mean that one is a good predictor of the other!

To compare ground truth with predictions, we always use \(R^2\).

OLS in Practice

OLS in Practice

First, we’ll look at a test case on synthetic data. We’ll use Scikit-Learn’s make_regression function.

from sklearn import datasets
X, y = datasets.make_regression(n_samples=100, n_features=20, n_informative=5, bias=0.1, noise=30, random_state=1)

And then use the statsmodels package to fit the model.

import statsmodels.api as sm

# Add a constant (intercept) to the design matrix
#X_with_intercept = sm.add_constant(X)
#model = sm.OLS(y, X_with_intercept)

model = sm.OLS(y, X)
results = model.fit()

---

And print the summary of the results.

print(results.summary())

                                 OLS Regression Results                                
=======================================================================================
Dep. Variable:                      y   R-squared (uncentered):                   0.969
Model:                            OLS   Adj. R-squared (uncentered):              0.961
Method:                 Least Squares   F-statistic:                              123.8
Date:                Wed, 22 Oct 2025   Prob (F-statistic):                    1.03e-51
Time:                        22:31:23   Log-Likelihood:                         -468.30
No. Observations:                 100   AIC:                                      976.6
Df Residuals:                      80   BIC:                                      1029.
Df Model:                          20                                                  
Covariance Type:            nonrobust                                                  
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
x1            12.5673      3.471      3.620      0.001       5.659      19.476
x2            -3.8321      2.818     -1.360      0.178      -9.440       1.776
x3            -2.4197      3.466     -0.698      0.487      -9.316       4.477
x4             2.0143      3.086      0.653      0.516      -4.127       8.155
x5            -2.6256      3.445     -0.762      0.448      -9.481       4.230
x6             0.7894      3.159      0.250      0.803      -5.497       7.076
x7            -3.0684      3.595     -0.853      0.396     -10.224       4.087
x8            90.1383      3.211     28.068      0.000      83.747      96.529
x9            -0.0133      3.400     -0.004      0.997      -6.779       6.752
x10           15.2675      3.248      4.701      0.000       8.804      21.731
x11           -0.2247      3.339     -0.067      0.947      -6.869       6.419
x12            0.0773      3.546      0.022      0.983      -6.979       7.133
x13           -0.2452      3.250     -0.075      0.940      -6.712       6.222
x14           90.0179      3.544     25.402      0.000      82.966      97.070
x15            1.6684      3.727      0.448      0.656      -5.748       9.085
x16            4.3945      2.742      1.603      0.113      -1.062       9.851
x17            8.7918      3.399      2.587      0.012       2.028      15.556
x18           73.3771      3.425     21.426      0.000      66.562      80.193
x19           -1.9139      3.515     -0.545      0.588      -8.908       5.080
x20           -1.3206      3.284     -0.402      0.689      -7.855       5.214
==============================================================================
Omnibus:                        5.248   Durbin-Watson:                   2.018
Prob(Omnibus):                  0.073   Jarque-Bera (JB):                4.580
Skew:                           0.467   Prob(JB):                        0.101
Kurtosis:                       3.475   Cond. No.                         2.53
==============================================================================

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.

The \(R^2\) value is very good. We can see that the linear model does a very good job of predicting the observations \(y_i\).

Note

The summary uses the uncentered version of \(R^2\) because, as the footnote says, the model does not include a constant to account for an intercept term. You can try uncommenting the line X_with_intercept = sm.add_constant(X) and see that the summary then uses the centered version of \(R^2\).

Aside: Summary Statistics

Here is what all the statistics in the summary table mean:

1. R-squared (Uncentered):

• Definition: Measures the proportion of the variation in the dependent variable that is explained by the model, without subtracting the mean of the dependent variable.
• Formula: \(R^2 (\text{uncentered}) = 1 - \frac{\sum (y_i - \hat{y}_i)^2}{\sum y_i^2}\)

where \(y_i\) is the actual value, and \(\hat{y}_i\) is the predicted value from the regression.

• Interpretation: Higher values (closer to 1) indicate a better fit, but this version of \(R^2\) can sometimes be misleading because it doesn’t account for the mean.

2. Adjusted R-squared (Uncentered):

• Definition: Adjusts the uncentered \(R^2\) to account for the number of predictors in the model, preventing overfitting by penalizing for adding more variables.
• Formula: \(R^2 (\text{adj, uncentered}) = 1 - \left( \frac{(1 - R^2 (\text{uncentered}))(n - 1)}{n - p} \right)\)

where \(n\) is the number of observations, and \(p\) is the number of predictors in the model.

• Interpretation: It is a more conservative measure of fit than the regular \(R^2\), particularly useful when comparing models with different numbers of predictors.

3. F-statistic:

• Definition: The F-statistic tests whether the overall regression model is significant, i.e., whether at least one of the predictors explains a significant amount of the variance in the dependent variable.
• Formula: \(F = \frac{R^2 (\text{uncentered}) / (p - 1)}{(1 - R^2 (\text{uncentered})) / (n - p)}\)

where \(p\) is the number of predictors, and \(n\) is the number of observations.

• Interpretation: A high F-statistic suggests that the model is statistically significant.

4. Prob (F-statistic):

• Definition: This is the p-value associated with the F-statistic. It indicates the probability that the observed F-statistic would occur if the null hypothesis (that none of the predictors are significant) were true.
• Interpretation: A small p-value (typically less than 0.05) suggests that the model is statistically significant, meaning that at least one predictor is important.

5. Log-Likelihood:

• Definition: The log-likelihood measures the likelihood that the model could have produced the observed data. It is a measure of the fit of the model to the data.
• Formula: \(\mathcal{L} = -\frac{n}{2} \log(2\pi \sigma^2) - \frac{1}{2\sigma^2} \sum (y_i - \hat{y}_i)^2\)

where \(\sigma^2\) is the variance of the residuals.

• Interpretation: A higher log-likelihood indicates a better fit of the model.

6. Akaike Information Criterion (AIC):

• Definition: AIC is a measure of the relative quality of a statistical model for a given set of data. It penalizes the likelihood function for adding too many parameters.
• Formula: \(\text{AIC} = 2p - 2 \log(\mathcal{L})\)

where \(p\) is the number of parameters, and \(\mathcal{L}\) is the log-likelihood.

• Interpretation: Lower AIC values suggest a better model fit, but it penalizes for overfitting.

7. Bayesian Information Criterion (BIC):

• Definition: Similar to AIC, BIC penalizes models with more parameters, but more strongly than AIC. It is used to select among models.

• Formula: \(\text{BIC} = p \log(n) - 2 \log(\mathcal{L})\)

where \(p\) is the number of parameters, \(n\) is the number of observations, and \(\mathcal{L}\) is the log-likelihood.

• Interpretation: A lower BIC indicates a better model, with stronger penalties for models with more parameters.

8. Coefficient Table:

• The first two columns are the independent variables and their coefficients. It is the \(m\) in \(y = mx + b\). One unit of change in the variable will affect the variable’s coefficient’s worth of change in the dependent variable. If the coefficient is negative, they have an inverse relationship. As one rises, the other falls.

• The std error is an estimate of the standard deviation of the coefficient, a measurement of the amount of variation in the coefficient throughout its data points.

• The t is related and is a measurement of the precision with which the coefficient was measured. A low std error compared to a high coefficient produces a high t statistic, which signifies a high significance for your coefficient.

• P>|t| is one of the most important statistics in the summary. It uses the t statistic to produce the P value, a measurement of how likely your coefficient is measured through our model by chance. For example, a P value of 0.378 is saying there is a 37.8% chance the variable has no affect on the dependent variable and the results are produced by chance. Proper model analysis will compare the P value to a previously established alpha value, or a threshold with which we can apply significance to our coefficient. A common alpha is 0.05, which few of our variables pass in this instance.

• [0.025 and 0.975] are both measurements of values of our coefficients within 95% of our data, or within two standard deviations. Outside of these values can generally be considered outliers.

The coefficient description came from this blog post which also describes the other statistics in the summary table.

---

Back to the example.

Some of the independent variables may not contribute to the accuracy of the prediction.

ax = ut.plotSetup3d(-2, 2, -2, 2, -200, 200)

# try columns of X with large coefficients, or not
ax.plot(X[:, 1], X[:, 2], 'ro', zs=y, markersize = 4)

Note that each parameter of an independent variable has an associated confidence interval.

If a coefficient is not distinguishable from zero, then we cannot assume that there is any relationship between the independent variable and the observations.

---

In other words, if the confidence interval for the parameter includes zero, the associated independent variable may not have any predictive value.

print('Confidence Intervals: {}'.format(results.conf_int()))
print('Parameters: {}'.format(results.params))

Confidence Intervals: [[  5.65891465  19.47559281]
 [ -9.44032559   1.77614877]
 [ -9.31636359   4.47701749]
 [ -4.12661379   8.15524508]
 [ -9.4808662    4.22965424]
 [ -5.49698033   7.07574692]
 [-10.22359973   4.08684835]
 [ 83.74738375  96.52928603]
 [ -6.77896356   6.75226985]
 [  8.80365396  21.73126149]
 [ -6.86882065   6.4194618 ]
 [ -6.97868351   7.1332267 ]
 [ -6.71228582   6.2218515 ]
 [ 82.96557061  97.07028228]
 [ -5.74782503   9.08465366]
 [ -1.06173893   9.85081724]
 [  2.02753258  15.5561241 ]
 [ 66.56165458  80.19256546]
 [ -8.90825108   5.0804296 ]
 [ -7.85545335   5.21424811]]
Parameters: [ 1.25672537e+01 -3.83208841e+00 -2.41967305e+00  2.01431564e+00
 -2.62560598e+00  7.89383294e-01 -3.06837569e+00  9.01383349e+01
 -1.33468527e-02  1.52674577e+01 -2.24679428e-01  7.72715974e-02
 -2.45217158e-01  9.00179264e+01  1.66841432e+00  4.39453916e+00
  8.79182834e+00  7.33771100e+01 -1.91391074e+00 -1.32060262e+00]

Find the independent variables that are not significant.

CIs = results.conf_int()
notSignificant = (CIs[:,0] < 0) & (CIs[:,1] > 0)
notSignificant

array([False,  True,  True,  True,  True,  True,  True, False,  True,
       False,  True,  True,  True, False,  True,  True, False, False,
        True,  True])

Let’s look at the shape of significant variables.

Xsignif = X[:,~notSignificant]
Xsignif.shape

(100, 6)

---

By eliminating independent variables that are not significant, we help avoid overfitting.

model = sm.OLS(y, Xsignif)
results = model.fit()
print(results.summary())

                                 OLS Regression Results                                
=======================================================================================
Dep. Variable:                      y   R-squared (uncentered):                   0.965
Model:                            OLS   Adj. R-squared (uncentered):              0.963
Method:                 Least Squares   F-statistic:                              437.1
Date:                Wed, 22 Oct 2025   Prob (F-statistic):                    2.38e-66
Time:                        22:31:23   Log-Likelihood:                         -473.32
No. Observations:                 100   AIC:                                      958.6
Df Residuals:                      94   BIC:                                      974.3
Df Model:                           6                                                  
Covariance Type:            nonrobust                                                  
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
x1            11.9350      3.162      3.775      0.000       5.657      18.213
x2            90.5841      2.705     33.486      0.000      85.213      95.955
x3            14.3652      2.924      4.913      0.000       8.560      20.170
x4            90.5586      3.289     27.535      0.000      84.028      97.089
x5             8.3185      3.028      2.747      0.007       2.307      14.330
x6            71.9119      3.104     23.169      0.000      65.749      78.075
==============================================================================
Omnibus:                        9.915   Durbin-Watson:                   2.056
Prob(Omnibus):                  0.007   Jarque-Bera (JB):               11.608
Skew:                           0.551   Prob(JB):                      0.00302
Kurtosis:                       4.254   Cond. No.                         1.54
==============================================================================

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Real Data: House Prices in Ames, Iowa

Let’s see how powerful multiple regression can be on a real-world example.

A typical application of linear models is predicting house prices.

Linear models have been used for this problem for decades, and when a municipality does a value assessment on your house, they typically use a linear model.

We can consider various measurable attributes of a house (its “features”) as the independent variables, and the most recent sale price of the house as the dependent variable.

---

For our case study, we will use the features:

• Lot Area (sq ft),
• Gross Living Area (sq ft),
• Number of Fireplaces,
• Number of Full Baths,
• Number of Half Baths,
• Garage Area (sq ft),
• Basement Area (sq ft)

So our design matrix will have 8 columns (including the constant for the intercept):

\[ X\beta = \mathbf{y}, \]

and it will have one row for each house in the data set, with \(y\) the sale price of the house.

We will use data from housing sales in Ames, Iowa from 2006 to 2009:

Ames Iowa

Tim Kiser (w:User:Malepheasant) CC BY-SA 2.5 via Wikimedia Commons

---

df = pd.read_csv('data/ames-housing-data/train.csv')

df[['LotArea', 'GrLivArea', 'Fireplaces', 'FullBath', 'HalfBath', 'GarageArea', 'TotalBsmtSF', 'SalePrice']].head()

	LotArea	GrLivArea	Fireplaces	FullBath	HalfBath	GarageArea	TotalBsmtSF	SalePrice
0	8450	1710	0	2	1	548	856	208500
1	9600	1262	1	2	0	460	1262	181500
2	11250	1786	1	2	1	608	920	223500
3	9550	1717	1	1	0	642	756	140000
4	14260	2198	1	2	1	836	1145	250000

---

Some things to note here:

• House prices are in dollars
• Areas are in square feet
• Rooms are in counts

Do we have scaling concerns here?

No, because each feature will get its own \(\beta\), which will correct for the scaling differences between different units of measure.

X_no_intercept = df[['LotArea', 'GrLivArea', 'Fireplaces', 'FullBath', 'HalfBath', 'GarageArea', 'TotalBsmtSF']]
X_intercept = sm.add_constant(X_no_intercept)
y = df['SalePrice'].values

Note

Note that removing the intercept will cause the \(R^2\) to go up, which is counter-intuitive. The reason is explained here] – but amounts to the fact that the formula for R2 with/without an intercept is different.

Let’s split the data into training and test sets.

from sklearn import utils, model_selection
X_train, X_test, y_train, y_test = model_selection.train_test_split(
    X_intercept, y, test_size = 0.5, random_state = 0)

Fit the model to the training data.

model = sm.OLS(y_train, X_train)
results = model.fit()
print(results.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.759
Model:                            OLS   Adj. R-squared:                  0.757
Method:                 Least Squares   F-statistic:                     325.5
Date:                Wed, 22 Oct 2025   Prob (F-statistic):          1.74e-218
Time:                        22:31:23   Log-Likelihood:                -8746.5
No. Observations:                 730   AIC:                         1.751e+04
Df Residuals:                     722   BIC:                         1.755e+04
Df Model:                           7                                         
Covariance Type:            nonrobust                                         
===============================================================================
                  coef    std err          t      P>|t|      [0.025      0.975]
-------------------------------------------------------------------------------
const       -4.285e+04   5350.784     -8.007      0.000   -5.34e+04   -3.23e+04
LotArea         0.2361      0.131      1.798      0.073      -0.022       0.494
GrLivArea      48.0865      4.459     10.783      0.000      39.332      56.841
Fireplaces   1.089e+04   2596.751      4.192      0.000    5787.515     1.6e+04
FullBath      1.49e+04   3528.456      4.224      0.000    7977.691    2.18e+04
HalfBath      1.56e+04   3421.558      4.559      0.000    8882.381    2.23e+04
GarageArea     98.9856      8.815     11.229      0.000      81.680     116.291
TotalBsmtSF    62.6392      4.318     14.508      0.000      54.163      71.116
==============================================================================
Omnibus:                      144.283   Durbin-Watson:                   1.937
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              917.665
Skew:                           0.718   Prob(JB):                    5.39e-200
Kurtosis:                       8.302   Cond. No.                     6.08e+04
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 6.08e+04. This might indicate that there are
strong multicollinearity or other numerical problems.

---

We see that we have:

• \(\beta_0\): Intercept of -$42,850
• \(\beta_1\): Marginal value of one square foot of Lot Area: $0.23
  • but NOTICE - this coefficient is not statistically different from zero!
• \(\beta_2\): Marginal value of one square foot of Gross Living Area: $48
• \(\beta_3\): Marginal value of one additional fireplace: $10,890
• \(\beta_4\): Marginal value of one additional full bath: $14,900
• \(\beta_5\): Marginal value of one additional half bath: $15,600
• \(\beta_6\): Marginal value of one square foot of Garage Area: $99
• \(\beta_7\): Marginal value of one square foot of Basement Area: $62

---

Is our model doing a good job?

There are many statistics for testing this question, but we’ll just look at the predictions versus the ground truth.

For each house we compute its predicted sale value according to our model:

\[ \hat{\mathbf{y}} = X\hat{\beta} \]

%matplotlib inline
from sklearn.metrics import r2_score

fig, (ax1, ax2) = plt.subplots(1,2,sharey = 'row', figsize=(12, 5))
y_oos_predict = results.predict(X_test)
r2_test = r2_score(y_test, y_oos_predict)
ax1.scatter(y_test, y_oos_predict, s = 8)
ax1.set_xlabel('True Price')
ax1.set_ylabel('Predicted Price')
ax1.plot([0,500000], [0,500000], 'r-')
ax1.axis('equal')
ax1.set_ylim([0, 500000])
ax1.set_xlim([0, 500000])
ax1.set_title(f'Out of Sample Prediction, $R^2$ is {r2_test:0.3f}')
#
y_is_predict = results.predict(X_train)
ax2.scatter(y_train, y_is_predict, s = 8)
r2_train = r2_score(y_train, y_is_predict)
ax2.set_xlabel('True Price')
ax2.plot([0,500000],[0,500000],'r-')
ax2.axis('equal')
ax2.set_ylim([0,500000])
ax2.set_xlim([0,500000])
ax2.set_title(f'In Sample Prediction, $R^2$ is {r2_train:0.3f}')
plt.show()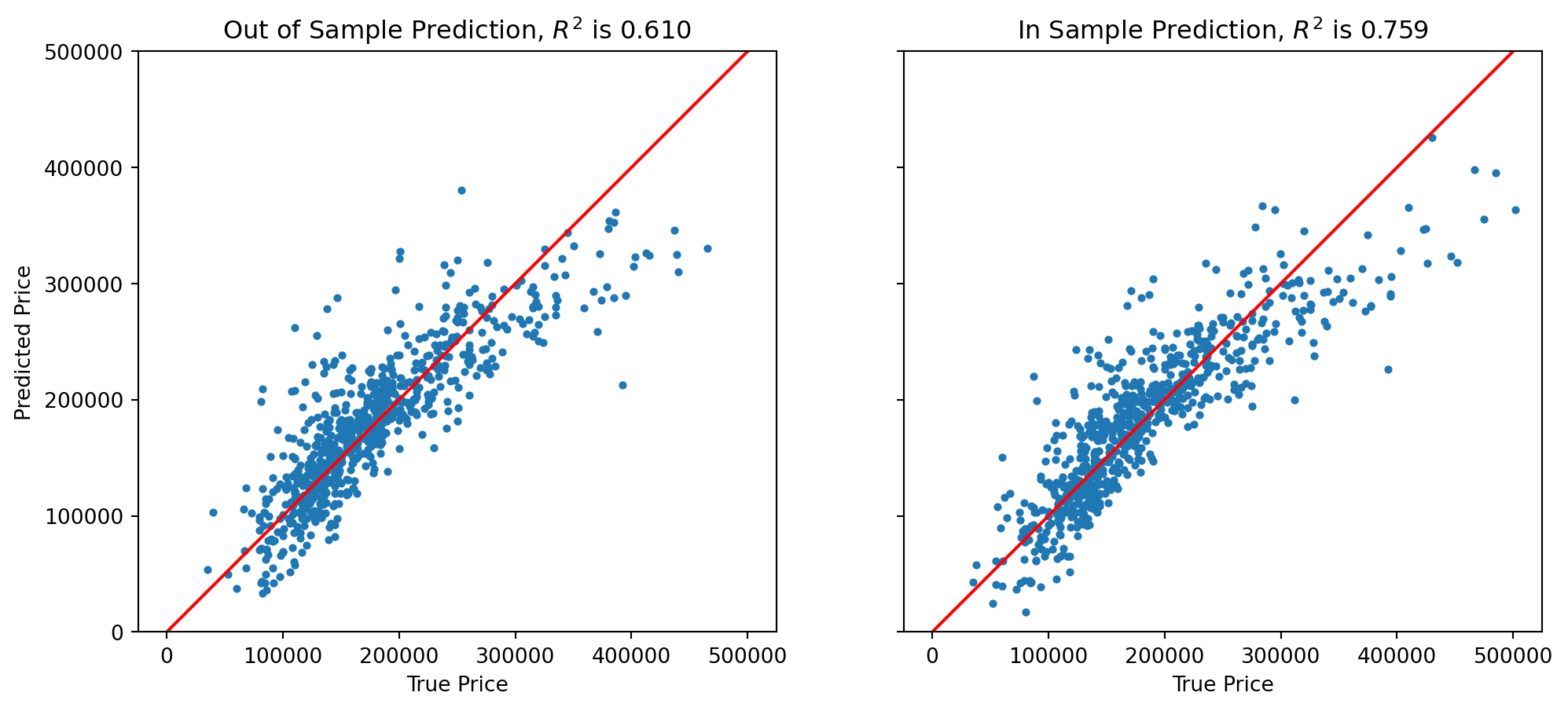

We see that the model does a reasonable job for house values less than about $250,000.

It tends to underestimate at both ends of the price range.

Note that the \(R^2\) on the (held out) test data is 0.610.

We are not doing as well on test data as on training data (somewhat to be expected).

For a better model, we’d want to consider more features of each house, and perhaps some additional functions such as polynomials as components of our model.

Recap

• Linear models are a powerful tool for prediction and inference
• The normal equations provide a simple way to compute the model coefficients
• The \(R^2\) statistic provides a simple measure of fit
• Careful use of the model is required to avoid overfitting