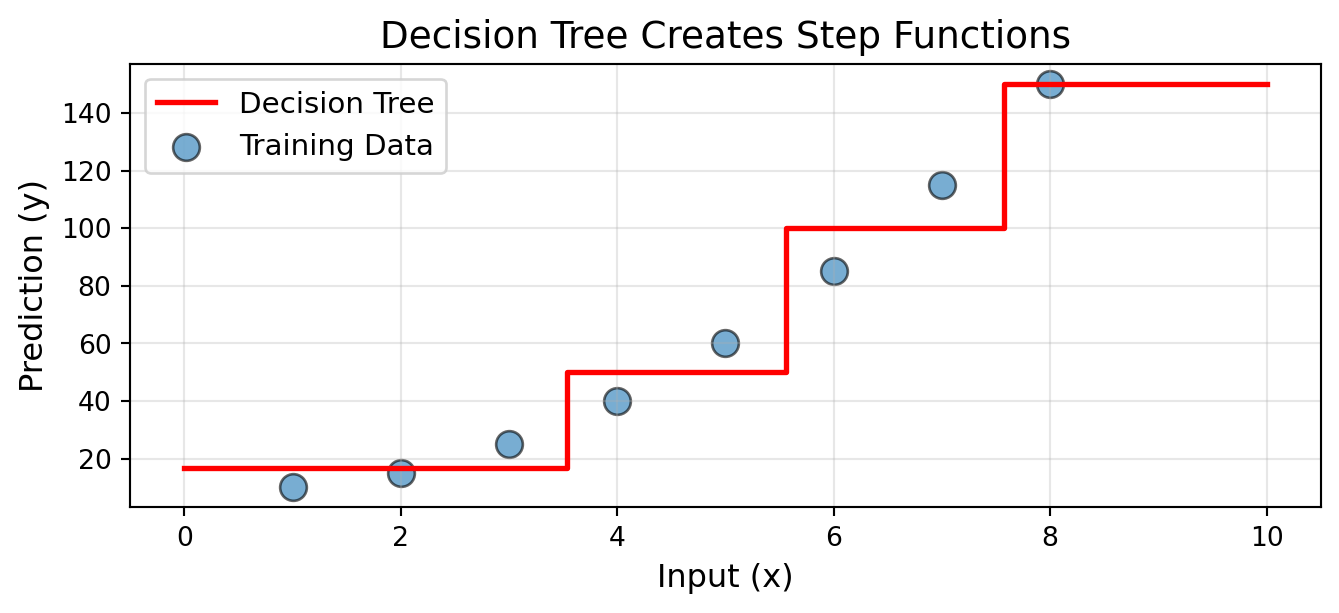
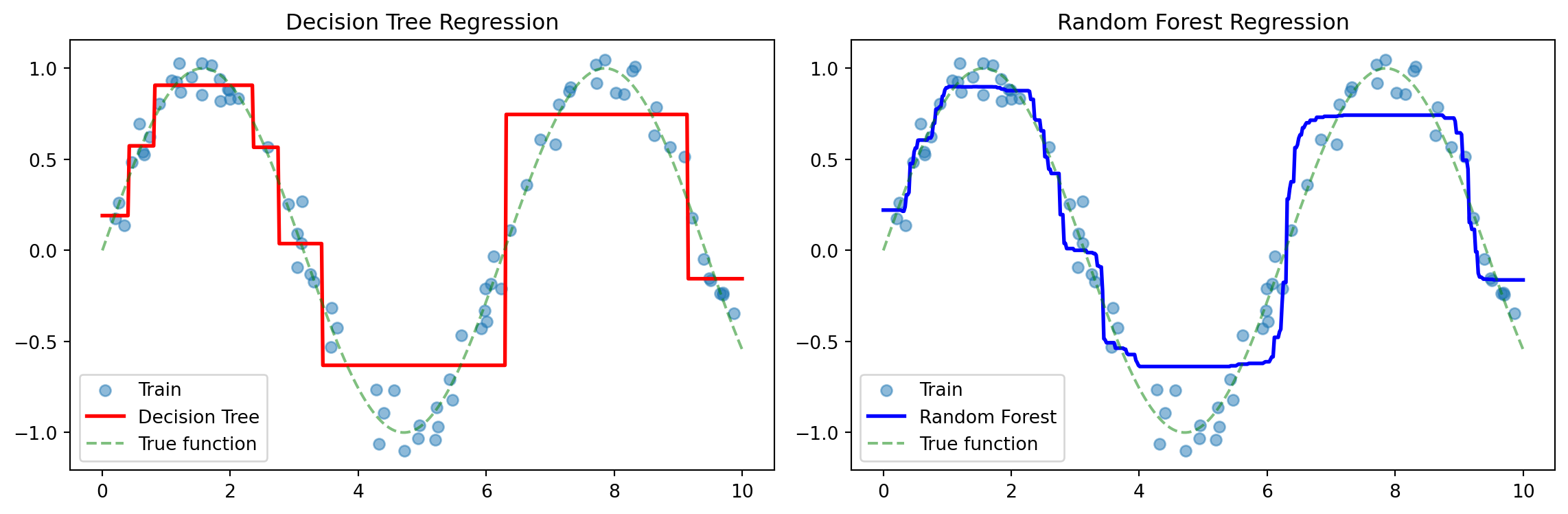
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
# Generate synthetic data: y = sin(x) + noise
np.random.seed(42)
X = np.sort(np.random.uniform(0, 10, 100)).reshape(-1, 1)
y = np.sin(X).ravel() + np.random.normal(0, 0.1, X.shape[0])
# Split data
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
# Single Decision Tree
dt = DecisionTreeRegressor(max_depth=3, random_state=42)
dt.fit(X_train, y_train)
y_pred_dt = dt.predict(X_test)
# Random Forest
rf = RandomForestRegressor(
n_estimators=100,
max_depth=3,
random_state=42
)
rf.fit(X_train, y_train)
y_pred_rf = rf.predict(X_test)
# Evaluate
print(f"Decision Tree R²: {r2_score(y_test, y_pred_dt):.3f}")
print(f"Random Forest R²: {r2_score(y_test, y_pred_rf):.3f}")
print(f"Decision Tree RMSE: {np.sqrt(mean_squared_error(y_test, y_pred_dt)):.3f}")
print(f"Random Forest RMSE: {np.sqrt(mean_squared_error(y_test, y_pred_rf)):.3f}")
# Visualize predictions
X_plot = np.linspace(0, 10, 500).reshape(-1, 1)
y_dt = dt.predict(X_plot)
y_rf = rf.predict(X_plot)
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.scatter(X_train, y_train, alpha=0.5, label='Train')
plt.plot(X_plot, y_dt, 'r-', linewidth=2, label='Decision Tree')
plt.plot(X_plot, np.sin(X_plot), 'g--', alpha=0.5, label='True function')
plt.legend()
plt.title('Decision Tree Regression')
plt.subplot(1, 2, 2)
plt.scatter(X_train, y_train, alpha=0.5, label='Train')
plt.plot(X_plot, y_rf, 'b-', linewidth=2, label='Random Forest')
plt.plot(X_plot, np.sin(X_plot), 'g--', alpha=0.5, label='True function')
plt.legend()
plt.title('Random Forest Regression')
plt.tight_layout()
plt.show()